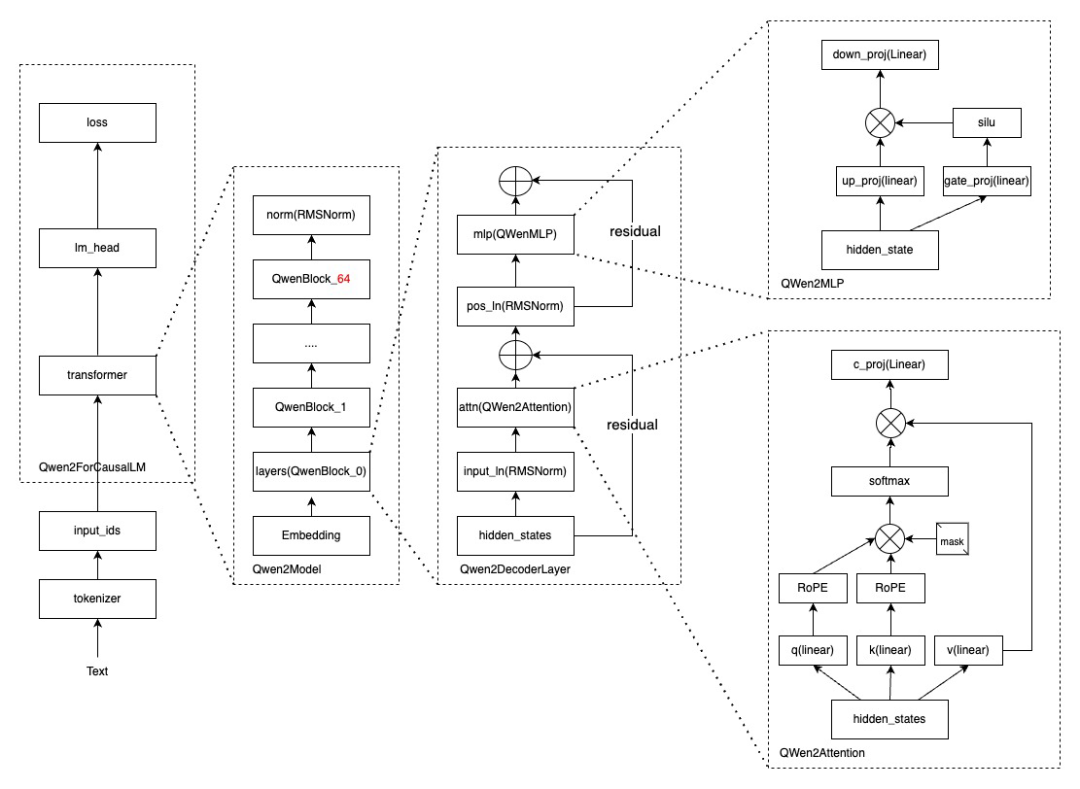
论文核心模型解析:Neural Social Physics (NSP)
NSP模型通过融合显式物理模型与深度神经网络,构建了一个统一的、端到端可训练框架,在预测精度、泛化性和可解释性之间取得了独特的平衡。
1.1 模型概述:融合物理与神经网络的混合架构
1.2 可微分物理核心:基于社交力模型的确定性动力学
社交力模型
受经典社交力模型启发的动力学系统,将行人运动抽象为受力驱动的过程
可学习参数
关键参数通过数据驱动方式学习,而非手工设定,增强模型适应性
可微分特性
确保物理核心能够嵌入神经网络并参与端到端训练
物理核心组成要素
驱动力 (Driving Force)
行人期望以某个舒适速度向其目标方向移动的倾向
排斥力 (Repulsive Force)
行人为了避免与其他行人或障碍物发生碰撞而产生的相互排斥的力
吸引力 (Attractive Force)
在群体同行时产生的相互吸引的力,保持群体凝聚力
1.3 神经网络校正器:基于变分自编码器的不确定性建模
功能定位
捕捉运动动力学和观测中的复杂不确定性,弥补物理核心在随机性建模方面的不足
协同工作
校正器补充物理核心无法捕捉的复杂行为模式,如个体意图、情绪和社会习惯等因素
1.4 模型架构与训练方法
神经微分方程框架
NSP模型基于神经微分方程框架,实现物理与网络的深度融合 [1]
整体架构
一个嵌入显式物理模型的深度神经网络,物理核心提供确定性的"骨架"轨迹,神经网络校正器添加随机性的"肌肉"和"皮肤"。
- 端到端可训练
- 统一框架设计
- 深度融合机制
训练方式
端到端的联合训练,同时优化物理模型参数和神经网络权重,确保物理核心和神经网络校正器能够相互适应、协同进化。
- 统一损失函数
- 协同优化
- 反向传播
"灰箱模型"范式在自动驾驶中的应用与优势
"灰箱模型"巧妙地介于纯物理(白箱)与纯数据驱动(黑箱)之间,通过结合物理模型的结构先验和数据驱动模型的学习能力,在物理约束和数据驱动之间寻求最佳平衡。
2.1 核心思想:物理约束与数据驱动的平衡
白箱模型
完全基于第一性原理构建,内部结构完全透明和可解释,但难以精确拟合复杂真实数据。
缺点:对现实简化过多
灰箱模型
NSP模型采用的方法,结合物理模型的结构先验和数据驱动模型的学习能力,取长补短。
优势:平衡精度与泛化
黑箱模型
纯数据驱动的模型,不关心内部物理机制,通过学习统计规律进行预测。
缺点:缺乏可解释性
设计哲学
物理定律提供可解释性和泛化性
物理定律为模型提供坚实的、可解释的"骨架",使预测结果符合物理常识,提升泛化能力。
- • 直观的物理解释
- • 普适性规律
- • 长尾场景鲁棒性
AI提升精度和适应性
深度学习从大规模数据中发现复杂模式,校准和优化物理模型参数,提升预测精度。
- • 复杂模式学习
- • 自适应校准
- • 持续进化能力
2.2 相对于传统模型的优势
对比纯物理模型
NSP模型具有更强的数据拟合能力与噪声处理能力。通过引入深度神经网络作为校正器,能够从数据中学习到复杂的噪声模式和随机行为。
物理核心参数通过数据学习,自适应调整内部参数
VAE校正器专门建模物理核心无法解释的残差部分
对比纯数据驱动模型
NSP模型具有更好的可解释性、泛化能力与物理合理性。显式的物理核心为模型提供强大的归纳偏置。
预测结果可分解为物理核心和神经网络部分
轨迹天然平滑合理,避免"穿墙"等错误
物理定律普适性保证未见过场景的合理预测
综合优势
在预测精度、泛化性和可解释性这三个关键维度上取得了精妙的平衡,成功缓解了传统机器学习中的权衡问题。
2.3 解决自动驾驶中的"预测魔咒"问题
"预测魔咒"挑战
长尾场景问题
自动驾驶系统在面对发生概率极低但种类繁多的复杂交通状况时,预测存在巨大不确定性,可能导致严重安全风险。
- • 突然冲到马路的儿童
- • 行为异常的醉酒者
- • 复杂路口的混合交通
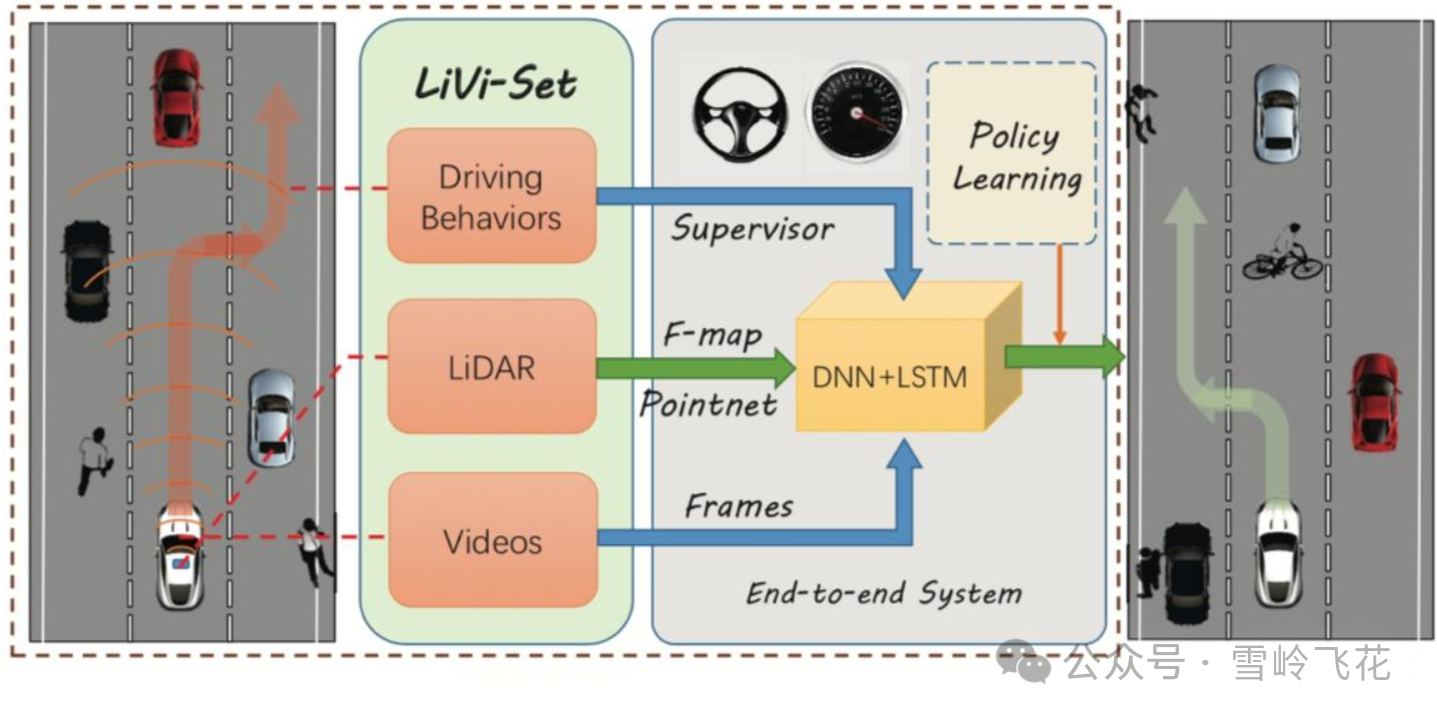
NSP应对策略
通过嵌入显式的物理约束,提升模型在极端或未知场景下的泛化能力。物理核心提供可靠的"最坏情况"估计基础。
实证结果
在高密度、未见场景下仍能保持合理的预测轨迹,显著减少碰撞。实验结果强有力证明物理核心在维持预测物理合理性方面的有效性。
自动驾驶场景中的具体实现与潜力
NSP框架在自动驾驶系统中作为"感知-预测-规划"流水线的关键组件,为车辆决策、规划和控制模块提供精准可靠的行人行为预测。
3.1 行人轨迹预测的实现方式
输入数据处理
历史轨迹
过去3秒,每秒10帧的二维坐标点序列
静态环境
高精地图数据,道路边界、车道线等
动态交通
周围车辆、行人、自行车的位置和轨迹
语义信息
行人朝向、姿态、类别等辅助信息
多模态输出
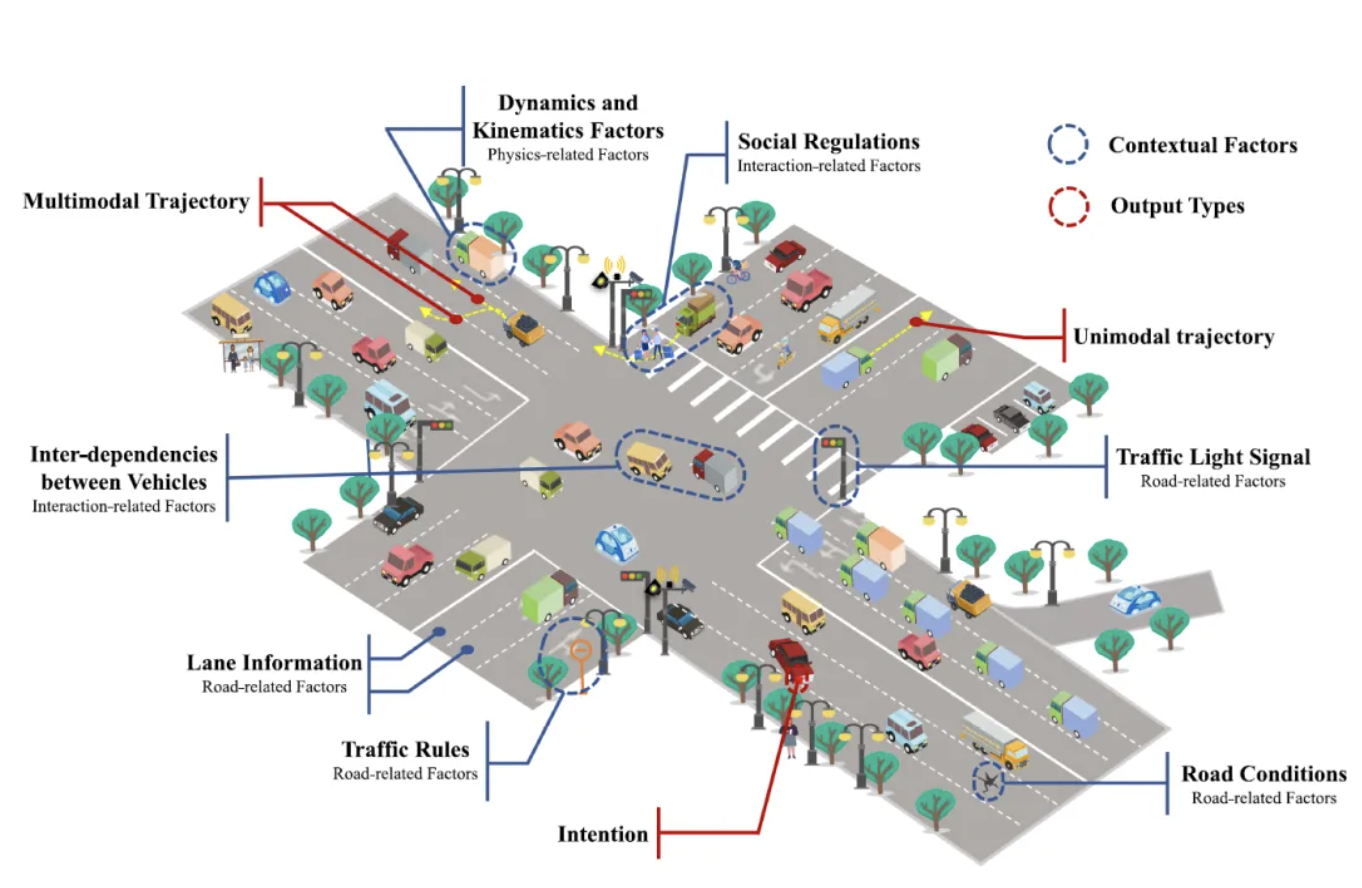
输出K条(如K=6)最有可能的未来轨迹,每条轨迹都是未来固定时长(如6秒)的坐标点序列,捕捉人类行为的不确定性。
场景应用实例
无信号交叉路口
准确判断行人是否有穿越马路的意图,预测其可能的穿越轨迹和时间。
- • 行人-车辆博弈分析
- • 避让行为预测
- • 安全通行时机判断
人车混行密集交通
学习复杂的群体行为模式,如跟随、超越、利用车辆间空隙穿行。
- • 人群"车道"效应
- • 复杂交互建模
- • 密度适应预测
特殊区域适应
学校、医院、商业区等行为模式各不相同,神经网络自适应调整。
- • 儿童行为预测
- • 紧急避让模式
- • 保守安全策略
3.2 模型的可解释性与分析能力
行为解释
通过显式物理模型分析行人运动背后的驱动力,如排斥力、吸引力等作用机制。
模型调试
利用物理模型的可解释性,诊断和修正预测错误,结构化定位问题根源。
仿真应用
生成符合物理规律的虚拟行人数据,用于训练和测试,特别是危险但罕见的"长尾"场景。
3.3 未来潜力与发展方向
框架通用性
NSP框架可扩展至其他交通参与者(如车辆、自行车)的预测,构建统一的、多智能体的交通场景预测系统。
机动车辆
二自由度或三自由度自行车模型作为物理核心
自行车
考虑倾斜和平衡的动力学模型
其他参与者
摩托车、电动车等多样化交通模式
物理模型演进
集成更复杂的物理模型以适应不同场景,如认知模型、博弈论模型、多尺度模型等。
考虑行人的感知、注意力和决策过程
描述交通参与者之间的交互策略
宏观流体力学与微观社会力相结合