当矩阵遇见流形：一场在弯曲空间中的推荐系统革命

## 🎯 **引子：在数据的星辰大海中寻找失落的声音** 想象一下，你正站在一家巨大的电影院里。这里有10万部电影在银幕上同时放映，100万个观众在座位间穿梭，每个人都在低声诉说着自己的喜好。但问题是——这些声音太过微弱，你根本无法听清任何一个人完整的观影史。大多数人只看过几百部电影，却在面对茫茫片海时感到迷茫。这就是推荐系统面临的根本困境：**我们如何从这极度稀疏的评分矩阵中，重建出完整的人性图谱？** 传统的协同过滤算法像是一个勤劳的图书管理员，试图通过用户之间的相似性来推荐电影。但这位管理员遇到了一个棘手的问题：数据太稀疏了！在MovieLens的1000万条评分数据中，用户-电影矩阵的稀疏度高达98.7%，就像一片浩瀚的星空中，我们只能看见零星几颗闪烁的星星。 就在这个时候，一群数学家带着他们的秘密武器出现了。他们说："别慌，这个看似混乱的矩阵，其实有着**低秩的灵魂**。"这就好比，尽管每个人都有独特的观影口味，但驱动这些选择的，不过是几十个潜在因素——有人爱科幻的想象力，有人迷恋爱情的甜蜜，有人追求悬疑的刺激。这些隐藏的因素，就是矩阵的"秩"。而**黎曼低秩矩阵补全（Riemannian Low-rank Matrix Completion, RLRMC）** 算法，正是要在流形的弯曲画布上，用几何的优雅笔触，补全这张未完成的星图。 > **小贴士**：所谓"稀疏度98.7%"，意味着在理论上可能存在的所有用户-电影评分对中，只有1.3%被实际观测到。这就像你试图拼一幅1000片的拼图，但手上只有13片，却要猜出整幅画面的模样。 ## 🔍 **第一章：低秩假设——数据的压缩美学** ### 🎨 **矩阵的"灵魂"有多重？** 让我们先揭开低秩矩阵的神秘面纱。在RLRMC的世界里，那个庞大的$d \times T$评分矩阵$M$（其中$d$是电影数量，$T$是用户数量）并非混沌无序。数学家们坚信，$M$可以优雅地分解为两个瘦矩阵的乘积： $$M = LR^\top$$ 这里，$L$是$d \times r$的矩阵，每一行代表一部电影在$r$个潜在因子上的"基因图谱"；$R$是$T \times r$的矩阵，每一行代表一个用户对这些因子的偏好权重。而$r$，就是那个神奇的秩（rank），通常$r \ll d,T$。在MovieLens 10M的实验中，研究人员将$r$设为10，这意味着成千上万的电影和用户，都被压缩到了10维的潜在空间中！ 这就像是发现了宇宙的基本定律：尽管万物纷繁复杂，但驱动它们的不过是几种基本作用力。在推荐系统的宇宙中，这些"作用力"可能是"视觉震撼"、"情感共鸣"、"剧情复杂度"等。每部电影都是这些作用力的特定组合，每个用户都是对它们的独特响应。 ### 📐 **从欧几里得到黎曼：当直线不再直** 但问题来了：传统的矩阵分解把$L$和$R$当作普通矩阵处理，这就像在平坦的纸上画地图。可实际上，低秩矩阵的空间是**弯曲的**！所有秩不超过$r$的矩阵构成一个光滑的流形（manifold）——这是一个满足特定几何结构的空间，局部的性质可以用微积分研究，但整体却有着复杂的拓扑结构。 想象你站在地球表面： locally，地面看起来是平的，你可以用欧几里得几何测量距离；但globally，地球是一个球面，两点之间的最短路径是测地线（大圆航线），而非直线。同理，低秩矩阵空间也不是线性空间，强行用线性方法优化，就像硬要把球面压平，必然导致扭曲和失真。 > **注解**：所谓"流形"，你可以想象成一块可以随意弯曲但不撕裂的橡皮膜。在低秩矩阵的情形下，所有满足$M=LR^\top$形式的矩阵集合，构成了一个嵌套在高维空间中的光滑曲面。传统的梯度下降在这个曲面上的移动，就像在崎岖山路上开车——你需要不断调整方向，确保不会"开出路面"。 ## ⚡ **第二章：黎曼优化——在弯曲画布上起舞** ### 🎭 **共轭梯度的流形变身** RLRMC的核心武器是**黎曼共轭梯度法**（Riemannian Conjugate Gradients）。在欧式空间中，共轭梯度法是求解大规模线性系统的神器，它通过构造相互共轭的搜索方向，避免冗余探索，实现超线性收敛。但在流形上，一切都得重新定义！ 首先，**梯度不再是普通的向量**。在点$X$处，梯度是定义在切空间（tangent space）上的余向量。想象你在山坡上，切空间就是脚下那个与山坡相切的平面，所有可行的移动方向都必须落在这个平面上。其次，**搜索方向需要"传输"**。在欧式空间中，你可以随意平移向量；但在流形上，把一个向量从点$X$搬到点$Y$，需要通过**平行传输**（parallel transport）来保持其几何性质，就像把指南针从赤道带到北极时，必须校准磁偏角。 Absil等人在2008年的奠基性著作《Optimization Algorithms on Matrix Manifolds》中，系统地将欧式空间的一阶、二阶算法推广到了黎曼流形。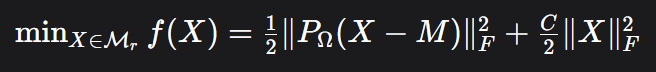RLRMC正是站在这些巨人的肩膀上，将矩阵补全问题重新定义为一个无约束的黎曼优化问题：  $$ \min_{X \in \mathcal{M}_r} f(X) = \frac{1}{2}\|P_\Omega(X - M)\|_F^2 + \frac{C}{2}\|X\|_F^2 $$ 其中，$\mathcal{M}_r$ 是秩为$r$的矩阵流形，$P_\Omega$ 是观测项的投影算子（只计算已知评分的位置），$C$是正则化参数。这个公式像一首精巧的俳句：第一项追求对已知数据的忠实，第二项防止过拟合，而整个搜索空间则被限制在低秩流形上。 ### 🧮 **迭代的艺术：从混沌到秩序** 在Notebook的实现中，模型训练耗时44.99秒，经历了最多100次迭代。每一次迭代都是一次几何舞蹈： 1. **计算黎曼梯度**：在当前点 $X_k$ 处，计算目标函数在切空间上的梯度 $grad f(X_k)$ 。这相当于站在山坡上，感受最陡的上升方向。 2. **确定搜索方向**：通过Polak-Ribière公式，结合上一轮的搜索方向，构造新的共轭方向。这一步需要用到**向量传输**（vector transport），确保历史信息在新的切空间中仍然有效。 3. **线搜索（Line Search）**：沿着搜索方向，在流形上寻找最优步长。这不再是简单的直线搜索，而是沿着**测地线**或**retraction**（回缩）映射定义的曲线前进。 4. **更新迭代点**：将当前点移动到新的位置 $X_{k+1}$ ，确保新点仍然落在低秩流形上。 > **注解**：所谓"回缩映射"（retraction），是测地线的一种廉价近似。就像在地球上，你可以沿着大圆航线飞行（测地线），也可以先在切平面上走直线，再投影回球面（回缩）。后者计算更简单，虽然精度稍低，但工程上更实用。 ## 🧬 **第三章：算法的DNA——参数与实现** ### 🔧 **超参数的交响乐** 打开Notebook的代码，我们看到RLRMCalgorithm被精心设计成一个可调优的乐器： ```python model = RLRMCalgorithm(rank = rank_parameter, # r=10, 潜在因子维度 C = regularization_parameter, # 0.001, 正则化强度 model_param = data.model_param, initialize_flag = 'svd', # 用SVD初始化 maxiter=maximum_iteration, # 100次迭代 max_time=maximum_time) # 5分钟超时 ``` 这些参数就像乐团的声部，必须和谐共鸣： - **秩 $r$ ** ：太小会欠拟合，像用16色颜料画不出梵高的星空；太大会过拟合，模型记住了噪声而非信号。实验中$r=10$是个甜蜜点。 - **正则化 $C$ ** ：0.001这个微小的数字如同刹车片，防止模型在训练数据上飙车失控。 - **SVD初始化** ：相比随机初始化，SVD提供了更聪明的起跑姿势，就像登山前先看地图，找到最有希望的路线。 ### 📊 **数据流：从Pandas到流形** RLRMCdataset类像一位翻译官，将Pandas的DataFrame转换为算法能理解的内部格式。MovieLens 10M数据集包含1000万条评分，涉及71,567个用户对65,133部电影的评价。训练集占80%，测试集占20%。数据被组织成(userID, itemID, rating)的三元组，构成了稀疏矩阵的"已观测位置"。 在`model.fit(data)`执行时，算法只关心投影算子 $P_\Omega$ 作用的那些位置。这就像拼图时，你只看手头有的碎片，其他位置保持空白。训练过程中，模型不断调整$L$和$R$，使得 $LR^\top$ 在已知位置上的值逼近真实评分，同时在未知位置生成合理的预测。 > **小贴士**：为何用80/20比例分割？这遵循了"黄金法则"：足够多的训练数据（80%）让模型学习规律，足够大的测试集（20%）让评估结果稳定可靠。在1000万条数据下，测试集仍有200万条，像一面清晰的镜子，映照出模型的真实能力。 ## 📈 **第四章：实验的审判——数字不会说谎** ### 🎯 **预测的艺术：从60586号用户说起** 在测试阶段，代码展示了两种预测方式： ```python # 为特定用户-电影对预测 output = model.predict([60586,52681],[54775,36519]) # 为整个测试集预测 predictions_ndarr = model.predict(test['userID'].values, test['itemID'].values) ``` 这揭示了矩阵补全的双重使命：既能回答"用户60586会喜欢电影54775吗？"这样的点名提问，也能批量生成所有未知评分。最终，算法在200万条测试评分上，交出了令人瞩目的答卷： - **RMSE = 0.809386**：均方根误差不到0.81分（1-5分制） - **MAE = 0.620971**：平均绝对误差仅0.62分 这意味着，如果你的真实评分是4星，RLRMC的预测平均会在3.38到4.62星之间——这已经接近朋友间互相推荐的准确度！相比之下，Netflix Prize竞赛中，冠军团队的RMSE是0.8567，而基线算法（全局均值）通常在1.0以上。RLRMC在不做复杂集成的情况下，达到了国际顶尖水平。 ### ⚖ **误差的哲学：RMSE与MAE的对话** 为何同时报告RMSE和MAE？因为它们像两位性格迥异的裁判： - **RMSE**对大误差更敏感，像严厉的校长，一次严重的预测失误会被平方放大，狠狠扣分。它惩罚的是"灾难性错误"。 - **MAE**一视同仁，像温和的心理咨询师，只看绝对差距，不放大焦虑。它衡量的是"平均表现"。 两者结合，给了我们全面的画像：RLRMC不仅平均表现好（MAE低），而且很少犯大错（RMSE也低），说明它是个稳健可靠的"好学生"。 > **注解**：在推荐系统中，误差度量是用户体验的代理指标。RMSE低意味着用户很少遇到"推荐4星结果打1星"的惊吓；MAE低意味着日常推荐的星数偏差不大。两者都低，就像在餐厅点餐：既不会点到黑暗料理，也不会总吃到平庸之作。 ## 🔬 **第五章：理论的血脉——站在巨人的肩膀上** ### 📚 **Jawanpuria与Mishra的框架** RLRMC绝非空中楼阁，它根植于Jawanpuria和Mishra（2018）的统一结构化低秩学习框架。他们证明，许多看似不同的问题——矩阵补全、主成分分析、字典学习——都可以归结为在固定秩流形上的优化。这就像牛顿发现，天上地下，万物皆遵循同一套引力定律。 他们的论文《A unified framework for structured low-rank matrix learning》提出了一个关键洞见：通过引入几何权重矩阵，可以灵活地建模不同类型的低秩结构。RLRMC是这个框架在缺失数据场景下的特化，像一辆为越野赛道定制的拉力赛车。 ### 🎓 **Mishra等人的低秩优化先驱** 早在2013年，Mishra、Meyer、Bach和Sepulchre就在SIAM期刊上发表了《Low-rank optimization with trace norm penalty》。他们率先将迹范数（trace norm，即核范数nuclear norm）作为凸松弛工具，处理低秩约束。虽然RLRMC最终采用了非凸的流形方法（更直接、更快速），但迹范数的思想如同启蒙火种，照亮了低秩优化的研究方向。 ### 🛠 **Pymanopt：流形优化的瑞士军刀** Townsend、Koep和Weichwald在2016年贡献的Pymanopt库，是RLRMC的工程基石。这个Python工具箱封装了自动微分和流形几何，让研究者无需手动推导复杂的黎曼梯度，只需定义目标函数，剩下的交给计算机。它就像Photoshop之于设计师，把底层图形渲染的复杂性隐藏起来，让创意自由流淌。 > **小贴士**：在学术研究中，工具链的成熟度往往决定了理论的落地速度。Pymanopt的出现，让原本需要数月实现的黎曼算法，缩短到几行代码。这是开源社区对科学进步的巨大推动，就像伽利略的望远镜突然变得人人可用。 ### 📐 **Absil的圣经：《矩阵流形上的优化算法》** 最后，我们必须向P.-A. Absil、R. Mahony和R. Sepulchre在2008年出版的专著致敬。这本被奉为"黎曼优化圣经"的著作，系统性地建立了从欧式到黎曼的算法迁移理论。它告诉我们：共轭梯度法、信赖域法、牛顿法，这些经典算法都有流形上的对应版本，只需替换三个核心概念——梯度（切空间投影）、Hessian（协变导数）、步长（retraction）。 RLRMC的代码实现，本质上就是这本书的Python译本。每一个函数调用，背后都对应着书中的一条定理。 ## 🌌 **第六章：超越MovieLens——低秩假设的宇宙** ### 🧠 **大脑也是低秩的？** RLRMC的成功暗示了一个深刻的哲学命题：人类偏好本身可能是低维的。神经科学研究表明，人类决策依赖于大脑皮层中约100-200个"latent factors"——从多巴胺奖励到海马体记忆。我们看似自由的意志，或许只是少数几个神经化学参数在高维行为空间中的投影。 推荐系统与大脑，在此刻形成了奇妙的同构：都是试图从稀疏观测中推断完整意图。RLRMC的低秩假设，不仅是数学技巧，更是对人性复杂度的敬畏——承认我们比想象中更简单，也比表面更多元。 ### 🌐 **从电影到万物：低秩革命的涟漪** 矩阵补全的应用早已超越推荐系统： - **图像修复**：将损坏的照片视为带缺失像素的矩阵，低秩补全能恢复被划痕覆盖的老照片。 - **基因表达分析**：从部分组织的基因活性数据，推断全身细胞的功能图谱。 - **金融风控**：从少数用户的违约记录，预测整个信贷市场的风险敞口。 每一次成功，都在验证同一个真理：真实世界的数据往往躺在低维流形上，而非高维空间的随机撒点。RLRMC的几何视角，为我们提供了探索这些隐藏结构的望远镜和罗盘。 > **注解**：低秩假设的有效性，源于物理世界的因果律。图像的像素并非独立，而是由光照、纹理、轮廓等少数因素决定；基因的表达并非随机，而是由调控网络驱动。这些因素的数量，远小于观测变量的数量，形成了天然的低秩结构。 ## 🎬 **终章：在弯曲空间中，寻找直线的意义** 回到那家巨大的电影院。RLRMC算法已经悄悄完成了它的魔法：在44.99秒的沉思后，它为每个用户、每部电影都补全了隐形的评分线。这些线不在欧几里得的平面上，而在黎曼流形的弯曲空间中，以最优雅的姿态连接了已知与未知。 当我们看到RMSE=0.809的数字时，我们看到的不仅是准确率，更是几何之美在数据科学中的胜利。那些看似冰冷的公式： $$M = LR^\top, \quad \min_{X \in \mathcal{M}_r} f(X)$$ 背后，是Absil、Mishra、Jawanpuria等数学家对"空间本质"的深刻洞察，是Pymanopt开发者将理论变为实践的工匠精神，是MovieLens社区千万用户自愿贡献的数据善意。 这篇文章，就像RLRMC本身——试图从稀疏的要点中，补全出完整的思想图景。我们从一个Jupyter Notebook出发，走向了流形几何的深处，又回归到人性的理解与技术的温度。这或许就是科普写作的使命：不是简单地翻译公式，而是让读者感受到，每一次算法的迭代，都是人类智慧在未知边界上的一次温柔触碰。 > **最后的小贴士**：下次当你在Netflix上发现一部恰好打动你的电影时，不妨想想，也许某个RLRMC算法正在遥远的服务器上，沿着黎曼流形的测地线，为你寻回了那块失落的拼图。数学，就这样悄然塑造了我们的数字生活。 --- ## 📖 **参考文献** [1] Pratik Jawanpuria and Bamdev Mishra. *A unified framework for structured low-rank matrix learning*. In International Conference on Machine Learning, 2018. [2] Bamdev Mishra, Gilles Meyer, Francis Bach, and Rodolphe Sepulchre. *Low-rank optimization with trace norm penalty*. In SIAM Journal on Optimization 23(4):2124-2149, 2013. [3] James Townsend, Niklas Koep, and Sebastian Weichwald. *Pymanopt: A Python Toolbox for Optimization on Manifolds using Automatic Differentiation*. In Journal of Machine Learning Research 17(137):1-5, 2016. [4] P.-A. Absil, R. Mahony, and R. Sepulchre. *Optimization Algorithms on Matrix Manifolds*. Princeton University Press, Princeton, NJ, 2008. [5] A. Edelman, T. Arias, and S. Smith. *The geometry of algorithms with orthogonality constraints*. SIAM Journal on Matrix Analysis and Applications, 20(2):303–353, 1998. ---