因果格拉斯曼(Causal Grassmann)序列建模架构深度研究
1. 核心数学概念与架构机制
因果格拉斯曼(Causal Grassmann)序列建模架构是一种新兴的、旨在替代传统Transformer模型中自注意力机制的深度学习框架。该架构的核心思想源于格拉斯曼几何(Grassmann Geometry),通过将序列中的标记(tokens)关系建模为格拉斯曼流形(Grassmann Manifold)上的几何流(Geometric Flows),从而实现对序列信息的有效捕捉和融合。与自注意力机制通过计算所有标记对之间的权重来构建一个高维、稠密的注意力矩阵不同,因果格拉斯曼架构采用了一种更为结构化和几何化的方法。它首先将每个标记的高维隐藏状态投影到一个低维空间,然后在这个低维空间中,将局部的标记对解释为二维子空间。这些子空间随后通过普吕克坐标(Plücker Coordinates)被编码为固定维度的向量,这些向量捕捉了标记对之间的几何关系。最后,这些几何特征通过一个门控混合模块(Gated Mixing Block)被融合回原始的隐藏状态中,完成信息的流动和更新。这种设计不仅在计算效率上具有显著优势,更重要的是,它将模型的核心操作从难以解释的高维张量空间转移到了一个具有明确数学结构的有限维流形上,为提升模型的可解释性开辟了新的道路 。
1.1 格拉斯曼流形(Grassmann Manifold)
格拉斯曼流形是几何学和拓扑学中的一个核心概念,它为描述和分析线性子空间提供了一个强大的数学框架。在因果格拉斯曼架构中,格拉斯曼流形扮演着至关重要的角色,它不仅是模型进行几何计算的“舞台”,更是实现模型可解释性的关键所在。通过将序列建模问题转化为流形上的几何问题,该架构能够利用微分几何和代数几何中的丰富工具来分析和理解模型的行为。
1.1.1 定义:Gr(m, D) 作为子空间的几何表示
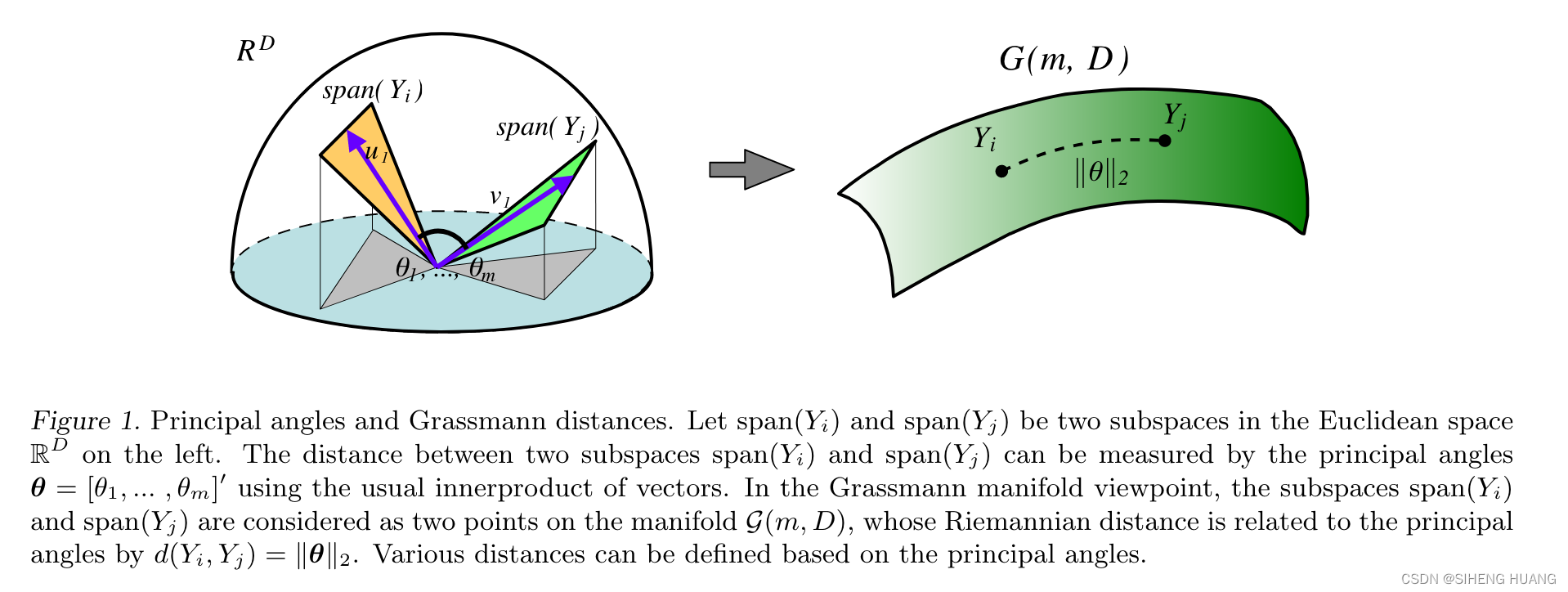
格拉斯曼流形,记作 Gr(m, D) ,是所有 D 维欧几里得空间中 m 维线性子空间的集合。这个集合本身可以被赋予一个光滑流形的结构,从而允许我们应用微分几何的工具来研究其性质。在因果格拉斯曼架构中,我们主要关注的是 Gr(2, r) ,即 r 维空间中的二维子空间。这个流形可以被看作是一个参数空间,其中的每个点都对应着一个二维平面。这种表示方法的优势在于,它将抽象的线性代数概念(子空间)转化为具体的几何对象(流形上的点),使得我们能够用几何直观来理解模型内部的表示。例如,在序列建模中,两个标记的嵌入向量可以张成一个二维子空间,这个子空间就可以被看作是格拉斯曼流形上的一个点。通过研究这个点在流形上的“轨迹”,即随着模型层数的增加,这个子空间如何变化,我们可以洞察模型是如何捕捉和整合序列信息的 。
格拉斯曼流形的几何结构由其上的黎曼度量所定义。这个度量在正交群的作用下保持不变,这意味着它只依赖于子空间本身,而不依赖于用于表示该子空间的具体基向量。这种内在的几何性质对于模型的鲁棒性和可解释性至关重要。例如,在因果格拉斯曼架构中,普吕克坐标作为格拉斯曼流形的嵌入表示,其几何意义和代数性质都源于这个内在的黎曼结构。通过利用格拉斯曼流形的几何结构,模型可以学习到对输入数据的特定变换(如基变换)具有不变性的特征表示,这有助于提高模型的泛化能力。此外,格拉斯曼流形上的测地线(geodesics)和曲率(curvature)等几何概念也为分析模型的动态行为提供了新的视角。例如,我们可以研究子空间在流形上的演化轨迹是否平滑,或者不同子空间之间的“距离”如何变化,从而量化模型在处理序列信息时的稳定性和差异性 。
1.1.2 作用:为模型提供一个有限维、结构化的计算空间
因果格拉斯曼架构的一个核心贡献在于,它将序列建模的核心操作从Transformer中无结构的高维张量空间转移到了一个有限维、具有丰富几何结构的格拉斯曼流形上。在Transformer中,自注意力机制通过计算一个 L x L 的注意力矩阵来捕捉所有标记对之间的关系,其中 L 是序列长度。这个矩阵可以看作是在一个非常高维的空间中进行操作,其维度与序列长度的平方成正比。这种高维性不仅带来了巨大的计算开销,也使得模型的行为难以分析和解释。因为在这个庞大的张量空间中,很难定义和追踪有意义的数学不变量来描述模型的全局行为 。
相比之下,因果格拉斯曼架构通过以下步骤构建了一个结构化的计算空间:
- 降维:首先,将每个标记的 d 维隐藏状态通过一个线性变换降维到 r 维空间,其中 r << d。这一步将计算的核心从高维的语义空间转移到了一个更易于处理的几何空间 。
- 子空间表示:在 r 维空间中,模型以因果的方式选取局部的标记对 ($z_t$, $z_{t+Δ}$),并将它们张成的二维子空间作为基本的计算单元。这个子空间是格拉斯曼流形 Gr(2, r) 上的一个点。
- 普吕克嵌入:通过普吕克坐标,将 Gr(2, r) 上的点嵌入到一个固定维度为 C(r, 2) 的欧几里得空间中。这个嵌入是有限维的,并且具有明确的代数结构。
通过这一系列操作,模型将原本复杂的、依赖于序列长度的成对交互问题,转化为一个在固定维度的格拉斯曼流形上进行的几何演化问题。这个计算空间是“有限维的”,因为其维度 C(r, 2) 是一个与序列长度 L 无关的常数。它也是“结构化的”,因为格拉斯曼流形具有丰富的几何和代数性质,例如黎曼度量、测地线和普吕克关系式。这种结构化的计算空间为模型的可解释性提供了坚实的基础。研究者可以利用微分几何和代数几何的工具来定义和分析模型行为的全局不变量,例如子空间在流形上的平均位置、曲率或跨层的稳定性统计量,从而更深入地理解模型的决策过程 。
1.2 普吕克坐标(Plücker Coordinates)
普吕克坐标是连接线性代数与几何学的一座重要桥梁,它为表示格拉斯曼流形上的点提供了一种具体而强大的工具。在因果格拉斯曼架构中,普吕克坐标扮演着将抽象的二维子空间转化为可计算、可比较的数值向量的关键角色。通过普吕克坐标,模型能够以一种几何不变的方式来编码标记对之间的关系,这是实现模型可解释性的核心机制之一。
1.2.1 定义:将二维子空间编码为固定维度的向量
普吕克坐标是一种用于表示射影空间中线性子空间的齐次坐标。具体来说,对于一个在 r 维空间中的二维子空间,它可以由两个线性无关的向量 v1 和 v2 张成。这个子空间的普吕克坐标是一个 C(r, 2) 维的向量,其分量是由 v1 和 v2 构成的 r x 2 矩阵的所有 2x2 子行列式。这里的 C(r, 2) 表示从 r 个元素中选取 2 个的组合数,即 r(r-1)/2。这个向量的维度是固定的,只取决于原始空间的维度 r,而与序列长度无关。这种固定维度的特性对于构建可扩展的神经网络架构至关重要 。
普吕克坐标的一个重要特性是它们是齐次的,即如果一个子空间由 (v1, v2) 张成,那么它也可以由 (av1 + bv2, cv1 + dv2) 张成,其中 ad - bc ≠ 0。这意味着普吕克坐标在子空间的基变换下会发生一个整体的缩放,但它们所表示的射影空间中的点是不变的。这种 “基不变性”或“几何不变性” 是普吕克坐标的核心优势。它确保了模型关注的是由两个向量张成的几何实体(子空间),而不是特定的向量表示。在因果格拉斯曼架构中,这意味着模型学习到的关系是关于标记对语义的内在几何关系,而不是依赖于它们在嵌入空间中的具体坐标。这使得模型的表示更加鲁棒,也更容易解释 。
1.2.2 计算:由局部标记对形成的矩阵的 2x2 子行列式构成
在因果格拉斯曼架构中,普吕克坐标的计算过程是模型前向传播的核心步骤之一。具体过程如下:
- 获取低维向量:首先,对于序列中的每个位置 t,模型通过线性降维得到其低维表示 $z_t ∈ R^r$ 。
- 形成局部对:为了遵循因果性原则,模型只考虑当前标记 t 与其之前的标记 t-Δ 形成的局部对 ($z_{t-Δ}, z_t$)。这里的 Δ 是一个预定义的偏移量,可以构成一个多尺度的窗口集合 。
- 构建矩阵:对于每一个局部对,模型将它们组合成一个 r x 2 的矩阵 $Z = [z_{t-Δ}, z_t]$。
- 计算子行列式:普吕克向量 p ∈ R^(C(r, 2)) 的每个分量 pij (其中 1 ≤ i < j ≤ r) 是通过计算矩阵 Z 的第 i 行和第 j 行构成的 2x2 子矩阵的行列式得到的。即 $p_ij = det([z_{t-Δ, i}, z_{t, i}; z_{t-Δ, j}, z_{t, j}])$ 。
这个过程可以高效地通过批处理操作在GPU上实现。计算出的普吕克向量 p 编码了由 z{t-Δ} 和 z
t 张成的二维子空间的几何信息。具体来说,普吕克向量的每个分量都反映了这两个向量在特定二维平面上的投影所张成的有向面积。因此,普吕克向量可以被看作是对两个标记之间语义关系的一种几何编码。这种编码方式不仅捕捉了它们之间的相似性或差异性,还保留了它们相互作用的方向性信息,为后续的特征融合提供了丰富的几何输入 。
1.2.3 不变性:在子空间基变换下保持不变,反映投影特性
普吕克坐标的几何不变性是其最重要的数学性质,也是因果格拉斯曼架构能够实现可解释性的根本原因。这种不变性体现在,如果两个不同的向量组 (v1, v2) 和 (v1', v2') 张成了同一个二维子空间,那么它们计算出的普吕克坐标 p 和 p' 在射影空间中是同一个点,即 p = k p',其中 k 是一个非零的标量。这意味着普吕克坐标所表示的几何信息是内在的,不依赖于用于张成子空间的具体基的选择 。
在因果格拉斯曼架构的上下文中,这种不变性具有深刻的意义。当模型处理一个标记对 (z
{t-Δ}, z
t) 时,它实际上是在分析由这两个向量定义的“语义方向”所张成的平面。普吕克坐标捕捉了这个平面的内在几何属性,例如它的“朝向”和“大小”。无论这两个向量在嵌入空间中如何旋转或缩放(只要它们仍然张成同一个平面),其普吕克坐标在射影空间中的表示都是不变的。这种特性使得模型的学习过程更加稳定和高效,因为它迫使模型关注于更高层次的、与具体坐标系无关的语义关系。
此外,普吕克坐标还满足一组称为 “普吕克关系式” 的二次方程。这些方程定义了格拉斯曼流形作为射影空间中的一个代数簇。这些代数约束为模型的行为提供了额外的结构。例如,它们可以用来验证计算出的普吕克向量是否有效,或者作为正则化项来引导模型学习更“几何合理”的表示。从可解释性的角度看,这些明确的代数关系使得我们可以利用代数几何的工具来分析和理解模型内部的表示,例如,通过研究普吕克向量在流形上的分布来发现模型学习到的语义模式。这与Transformer中注意力矩阵的无约束、高维特性形成了鲜明对比,后者的分析通常依赖于启发式的方法,缺乏坚实的数学基础 。
1.3 因果格拉斯曼混合层(Causal Grassmann Mixing Layer)
因果格拉斯曼混合层是该架构的核心组件,它取代了传统Transformer中的自注意力模块。这个混合层的设计精巧地结合了降维、几何编码和特征融合三个步骤,以一种高效且可解释的方式实现了序列信息的流动。整个流程遵循因果性原则,确保了模型可以用于自回归任务,如语言建模。
1.3.1 降维:将高维隐藏状态映射到低维空间
在因果格拉斯曼混合层的开始,模型首先对每个标记的隐藏状态进行降维处理。给定一个长度为 L 的序列,其隐藏状态矩阵为 H ∈ R^(L x d),其中 d 是模型的隐藏维度。对于每个位置 t 的隐藏状态 h
t ∈ R^d,模型通过一个可学习的线性变换
Wdown ∈ R^(d x r) 将其映射到一个低维空间,得到
zt = Wdown ht ∈ R^r。这里,r 是降维后的维度,且通常远小于 d (r << d) 。
这个降维步骤有几个重要的作用。首先,它显著降低了后续计算的复杂度。在格拉斯曼流形上进行操作的成本与空间的维度 r 密切相关,而不是原始的隐藏维度 d。通过将维度从 d 降低到 r,模型可以在一个更紧凑、更高效的空间中进行核心的几何计算。其次,降维可以看作是一种信息压缩和特征提取的过程。线性变换 Wdown 可以学习到如何将高维的语义信息投影到一组更具判别性的低维方向上。这些低维向量 zt 将作为构建局部子空间的基本元素,因此,降维的质量直接影响到模型捕捉序列关系的能力。最后,降维也是实现模型可解释性的第一步。通过将复杂的 d 维表示简化为 r 维表示,我们为后续的几何分析奠定了基础,使得研究者可以更容易地可视化和理解模型内部的表示动态 。
1.3.2 局部对形成:以因果方式组合局部标记对
在获得每个标记的低维表示 $z_t$ 之后,模型的下一步是形成用于几何编码的局部标记对。为了确保模型遵循因果性,即当前位置的计算只能依赖于过去的信息,模型在形成标记对时采用了因果窗口。具体来说,对于序列中的每个位置 t,模型会考虑一组预定义的偏移量集合 $W = {Δ_1, Δ_2, ..., Δ_m}$。对于每个偏移量 Δ ∈ W,模型形成一个标记对 ($z_{t-Δ}, z_t$)。这里的 Δ 必须是正数,以确保 $z_{t-Δ}$ 是在 $z_t$ 之前生成的 。
这种局部对的形成机制有几个优点。首先,它使得模型的计算复杂度与序列长度 L 成线性关系。因为对于每个位置 t,模型只考虑 m 个局部邻居,而不是像自注意力机制那样考虑所有 L 个位置。这使得模型在处理长序列时具有巨大的效率优势。其次,局部性假设在许多自然语言处理任务中是合理的。语言的局部性原理指出,一个词的含义在很大程度上受到其邻近词的影响。通过关注局部窗口内的标记对,模型可以有效地捕捉到短语级别的语法和语义信息。此外,通过使用多尺度的偏移量集合 W,模型可以同时捕捉不同范围内的局部依赖关系,例如,小的 Δ 可以捕捉紧密的语法关系,而大的 Δ 可以捕捉稍长一些的上下文信息。这种多尺度的局部建模能力使得模型在保持计算效率的同时,也能够获得丰富的上下文表示 。
1.3.3 几何特征融合:将普吕克坐标编码的几何特征混回表示
在形成局部标记对并计算出其普吕克坐标之后,因果格拉斯曼混合层的最后一步是将这些几何特征融合回原始的隐藏状态中。这个过程通过一个门控混合模块(Gated Mixing Block) 来完成,其设计类似于Transformer中的前馈网络(Feed-Forward Network),但输入是普吕克坐标编码的几何信息。
具体来说,对于位置 t,模型首先收集所有由偏移量集合 W 生成的普吕克向量 ${p_{t,Δ} | Δ ∈ W}$。这些向量被拼接起来,然后通过一个可学习的线性变换 $W_up$ 映射回原始的隐藏维度 d。这个过程可以看作是将从局部几何关系中提取的特征进行整合和转换,使其能够与原始的隐藏状态 $h_t$ 进行融合。融合的方式通常采用门控机制,例如,模型可以生成一个更新门 $u_t = σ(W_u * [h_t, p_t])$,其中 $p_t$ 是融合后的几何特征向量,σ 是sigmoid函数。最终的输出 $h'_t$ 则是原始状态和新特征的加权组合:$h'_t = u_t * h_t + (1 - u_t) * (W_p * p_t)$,其中 $W_p$ 是另一个可学习的投影矩阵。
这种门控融合机制允许模型自适应地决定在每个位置应该保留多少原始信息,以及应该融入多少从局部几何关系中提取的新信息。这使得模型能够灵活地处理不同类型的序列和任务。通过将几何特征融合回隐藏状态,信息得以在序列中流动和传播。每一层都对局部子空间进行微小的“变形”或“更新”,通过多层堆叠,模型就能够构建出对整个序列的复杂而深刻的理解。整个因果格拉斯曼混合层的设计,从降维到几何编码,再到门控融合,形成了一个完整而高效的信息处理流水线,它在不依赖显式注意力权重的情况下,实现了对序列关系的有效建模 。
2. 与Transformer的对比分析
因果格拉斯曼架构作为一种新兴的序列建模方法,其设计初衷就是为了挑战和替代当前在自然语言处理领域占据主导地位的Transformer架构。两者在核心机制、计算效率、性能表现和可解释性等方面存在着显著的差异。深入分析这些差异,不仅有助于我们理解因果格拉斯曼架构的优势和潜力,也能揭示其在未来发展中可能面临的挑战。
| 特性维度 | Transformer (自注意力机制) | Causal Grassmann (格拉斯曼混合层) |
|---|
| **核心机制** | 计算所有标记对之间的注意力权重,形成一个 L x L 的稠密矩阵。 | 将局部标记对映射到格拉斯曼流形上的点,并用普吕克坐标编码其几何关系。 |
| **计算复杂度** | **O(L²d)**,其中 L 是序列长度,d 是隐藏维度。二次方复杂度限制了长序列处理能力。 | **O(Lmr²)**,其中 m 是局部窗口大小,r 是降维后的维度。线性复杂度使其在处理长序列时具有天然优势 。 |
| **可解释性** | **低**。高维、无结构的注意力张量难以分析,缺乏全局行为的不变量。 | **高**。基于有限维格拉斯曼流形,便于定义和追踪全局几何不变量(如轨迹、曲率),提供结构化的分析框架 。 |
| **性能 (初步)** | 在各类任务上表现优异,尤其是在大规模模型和数据集上。 | 在中小规模模型(13-18M参数)上,性能已与Transformer相当,甚至在特定任务(如NLI)上略有超越 。 |
| **主要优势** | 强大的全局依赖建模能力,成熟的生态系统和预训练模型。 | 计算效率高,可解释性强,为序列建模提供了全新的几何视角。 |
| **主要挑战** | 计算和内存开销大,可解释性差。 | 模型成熟度低,大规模性能有待验证,需要专门的工程实现和可解释性工具。 |
Table 1: Transformer与Causal Grassmann架构的核心对比
2.1 可解释性(Explainability)
可解释性是当前深度学习领域,尤其是大型语言模型研究中,一个备受关注的核心问题。Transformer模型虽然在性能上取得了巨大成功,但其内部的决策过程往往被视为一个“黑箱”,难以理解和解释。因果格拉斯曼架构正是从这一痛点出发,试图通过引入几何结构来提升模型的透明度和可解释性。
2.1.1 Transformer的不可解释性:源于高维、无结构的注意力张量
Transformer模型的核心是自注意力机制,它通过计算一个 L x L 的注意力矩阵来捕捉序列中所有标记对之间的相互关系。这个注意力矩阵可以被视为一个高维张量,其维度随着序列长度的平方而增长。论文《Attention Is Not What You Need》的作者将这种操作重新解释为 “张量提升”(tensor lifting) :模型将每个标记的隐藏向量从一个相对低维的表示空间(例如 R^d)提升到了一个极高维的成对交互空间(例如 R^(L x L)) 。
这种“张量提升”机制是Transformer强大表达能力的来源,但同时也是其不可解释性的根源。首先,这个高维张量空间是 “无结构的” ,或者说,它缺乏明确的数学约束。注意力矩阵中的每个元素都是一个独立的、可学习的参数,它们之间除了通过softmax归一化保证行和为1之外,几乎没有其他数学关系。这使得我们很难用一个小的、显式的数学不变量族来描述模型的全局行为。虽然我们可以可视化单个注意力头在某一层的注意力图,但要将这些分散的、高维的注意力图聚合成一个连贯的、全局的模型行为图景,几乎是不可能的。作者认为,大型Transformer模型“不可解释性”的一个核心来源,并非仅仅是其巨大的规模,而是其核心操作——高维张量提升——在数学上是 “不可追踪的”(non-traceable) 。模型的核心计算发生在一个抵抗简洁解析描述的高维张量空间中,这使得我们难以从根本上理解模型是如何进行推理和决策的。
2.1.2 Causal Grassmann的优势:基于有限维流形,便于定义全局不变量
与Transformer的无结构张量空间形成鲜明对比,因果格拉斯曼架构将模型的核心计算置于一个有限维、具有丰富数学结构的格拉斯曼流形上。这一转变是其提升可解释性的关键。在因果格拉斯曼模型中,序列的交互不再是任意的、高维的张量操作,而是被约束为格拉斯曼流形上的 “受控变形”(controlled deformations) 。
具体来说,模型将每个标记对的低维表示 (z{t-Δ}, zt) 映射到格拉斯曼流形 Gr(2, r) 上的一个点。这个流形是有限维的,其维度为 2(r-2),远小于Transformer中 L x L 的注意力矩阵维度(当 L 很大时)。更重要的是,格拉斯曼流形是一个 “数学上刚性的”(mathematically rigid) 空间,它拥有明确的黎曼度量和代数结构。这意味着模型在流形上的每一步操作都受到严格的几何约束。例如,子空间的演化必须遵循测地线方程,普吕克坐标必须满足特定的代数关系式。这种结构化的计算环境为定义和分析模型的全局行为提供了可能。研究者不再面对一个庞大而混乱的注意力张量云,而是可以研究一条在格拉斯曼流形上清晰定义的“轨迹”。这条轨迹代表了模型在处理序列时,其内部表示在语义空间中的演化路径。通过分析这条轨迹的几何属性,如长度、曲率、与特定语义原型的距离等,我们可以获得对模型决策过程的深刻洞察。因此,将计算核心从张量空间转移到流形,为模型的可解释性提供了一个更具希望的“故事” 。
2.1.3 解释性不变量:普吕克向量作为候选,数量有限且遵循代数关系
在因果格拉斯曼架构中,普吕克向量被提议作为模型行为的候选 “解释性不变量”(explanatory invariants) 。这些不变量是理解模型内部工作机制的有力工具。与Transformer中难以捉摸的注意力权重相比,普吕克向量具有几个显著的优势,使其更适合作为解释模型的基础 。
首先,普吕克向量的数量是 “有限的” 。在每一层,对于每个标记,模型只生成与偏移量集合 W 数量相等的普吕克向量。这些向量的维度是固定的 C(r, 2)。这种有限性使得对它们进行系统性的分析和比较成为可能。我们可以追踪特定普吕克向量在模型不同层之间的变化,或者比较不同标记对对应的普吕克向量在流形上的分布,从而发现模型学习到的模式。
其次,普吕克向量 “遵循明确的代数关系” 。如前所述,普吕克坐标必须满足一组二次方程,这些方程定义了格拉斯曼流形作为射影空间中的一个代数簇。这些代数约束为模型的行为提供了额外的解释维度。例如,我们可以利用这些关系来验证模型的输出是否在几何上是合理的,或者设计新的正则化项来引导模型学习更符合我们期望的几何结构。
最后,普吕克向量是 “跨层可比较的” 。由于普吕克坐标是格拉斯曼流形的标准嵌入,不同层计算出的普吕克向量可以直接进行比较。这使得我们可以研究模型在处理序列时,其内部几何表示的演化动态。例如,我们可以分析一个子空间在流形上的“速度”和“加速度”,或者研究不同子空间之间的“距离”如何随着层数的增加而变化。这种跨层的可比性为理解深度模型的层级特征学习提供了新的途径。未来的研究方向包括系统地研究普吕克坐标、模型行为和人类可理解模式之间的相关性,目标是定义出比原始注意力图更稳定、更具解释力的不变量 。
2.2 计算效率(Computational Efficiency)
计算效率是序列模型能否应用于实际场景的关键因素,尤其是在处理长序列时。Transformer的自注意力机制虽然强大,但其二次方的计算复杂度一直是其主要的瓶颈。因果格拉斯曼架构通过其独特的设计,在计算效率上实现了显著的突破。
2.2.1 Transformer的复杂度:自注意力机制的二次方复杂度 O(L²)
Transformer模型的核心是自注意力机制,其计算过程可以分解为以下几个步骤:
- 生成Q, K, V矩阵:对于输入序列 H ∈ R^(L x d),通过三个可学习的线性变换 WQ, WK, WV 生成查询(Query)、键(Key)和值(Value)矩阵 Q, K, V ∈ R^(L x d)。这一步的计算复杂度是 O(L d^2)。
- 计算注意力分数:计算 Q 和 K 的转置的乘积,得到注意力分数矩阵 A = Q K^T ∈ R^(L x L)。这一步的计算复杂度是 O(L^2 d)。
- 缩放和Softmax:对注意力分数矩阵进行缩放(除以 sqrt(d)),然后对每一行应用softmax函数,得到注意力权重矩阵。这一步的计算复杂度是 O(L^2)。
- 加权求和:将注意力权重矩阵与 V 矩阵相乘,得到最终的输出。这一步的计算复杂度是 O(L^2 d)。
综合来看,自注意力机制的计算复杂度主要由
O(L^2 d) 决定。当序列长度 L 很大时,这个二次方的复杂度会带来巨大的计算和内存开销,使得Transformer难以处理非常长的文档或序列。为了解决这个问题,研究者们提出了各种稀疏注意力机制,如Longformer、BigBird等,它们通过限制注意力矩阵中的非零元素数量来降低复杂度,但这也可能牺牲模型的表达能力。
2.2.2 Causal Grassmann的复杂度:线性复杂度 O(L)(固定秩和窗口大小)
因果格拉斯曼架构在设计上就避免了二次方的计算复杂度。其计算过程可以分解为以下几个步骤:
- 降维:将每个标记的隐藏状态 ht ∈ R^d 降维到 zt ∈ R^r。这一步的计算复杂度是 O(L d r)。
- 形成局部对并计算普吕克坐标:对于每个位置 t,模型考虑 m 个偏移量,形成 m 个局部对。对于每个局部对,计算其普吕克坐标。计算一个普吕克坐标的复杂度是 O(r^2)。因此,这一步的总复杂度是 O(L m r^2)。
- 融合特征:将普吕克坐标编码的特征融合回隐藏状态。这一步的复杂度是 O(L m C(r,2) d)。
综合来看,因果格拉斯曼混合层的计算复杂度主要由
O(L (dr + mr^2 + mC(r,2)d)) 决定。由于 r, m, d 都是与序列长度 L 无关的常数,因此整个混合机制的复杂度是线性的,即
O(L)。这与Transformer的 O(L^2) 复杂度形成了鲜明对比。
这种线性复杂度使得因果格拉斯曼架构在处理长序列时具有天然的优势。它不需要引入额外的稀疏性假设,就能够以较低的计算成本处理任意长度的序列。这对于许多需要长程依赖建模的NLP任务,如长文档摘要、对话系统和代码生成等,具有非常重要的应用价值。论文的作者也指出,实现理论上的线性扩展需要专门的工程优化,例如融合的格拉斯曼核和优化的GPU算子,这将是未来工作的一个重要方向 。
2.3 性能(Performance)
尽管因果格拉斯曼架构在可解释性和计算效率上展现出巨大潜力,但其最终能否在实际应用中取代或补充Transformer,还取决于其性能表现。初步的实验结果表明,在中小规模的模型和数据集上,因果格拉斯曼架构已经能够与Transformer相媲美,甚至在某些特定任务上略有超越。
2.3.1 实验结果:在Wikitext-2和SNLI数据集上与Transformer性能相当
论文《Attention Is Not What You Need》在两个经典的NLP基准测试上对因果格拉斯曼架构进行了评估:语言建模(Wikitext-2)和自然语言推理(SNLI)。
在Wikitext-2数据集上的语言建模任务中,作者训练了一个纯粹的、基于因果格拉斯曼的语言模型。该模型包含13-18M个参数。实验结果显示,这个纯格拉斯曼模型在验证集上的困惑度(perplexity)与一个规模相当的Transformer基线模型相比,差距在10-15%以内。虽然性能上略有落后,但考虑到这是一个全新的、未经充分调优的架构,能够取得如此接近的结果已经令人印象深刻。这表明,即使没有显式的自注意力机制,基于格拉斯曼流的局部几何演化规则也足以学习到有效的语言模型 。
在SNLI(Stanford Natural Language Inference)数据集上的自然语言推理任务中,作者采用了一种不同的评估方式。他们将一个因果格拉斯曼分类头(classification head)接在一个固定的预训练模型(DistilBERT)的顶部,并与一个传统的Transformer分类头进行比较。在这种设置下,格拉斯曼分类头在验证集和测试集上的准确率都略微优于Transformer分类头。具体来说,最佳验证准确率分别为 0.8550 vs 0.8545,测试准确率分别为 0.8538 vs 0.8511。这个结果有力地证明了,当主干网络固定时,引入显式的几何结构(格拉斯曼混合)能够为特定的下游任务带来性能上的提升。这表明几何视角不仅具有哲学上的吸引力,在实践中也是有用的 。
2.3.2 模型规模:在13-18M参数规模下展现出竞争力
目前关于因果格拉斯曼架构的实验主要集中在中小规模的模型上(13-18M参数)。在这些规模上,该架构已经展现出了与Transformer相当的竞争力。然而,Transformer的成功很大程度上归功于其在更大规模(数十亿甚至数千亿参数)和数据集上的“扩展定律”(scaling laws)。因此,一个关键的问题是,因果格拉斯曼架构的性能是否也能随着模型规模的增大而持续提升,以及它在大规模下的表现能否与Transformer相匹敌。
论文的作者也承认,他们目前的模型在语言建模任务上并未超越Transformer,这并不令人意外,因为他们的设计相对简单,并且缺乏大规模的超参数调优。未来的工作需要测试该架构在更大规模和更具挑战性的推理基准上的表现。这包括开发高效的工程实现,以将理论上的线性复杂度优势在实践中发挥出来,以及探索更丰富的格拉斯曼结构,例如超越 k=2 的子空间,或者研究能够鼓励在格拉斯曼流形上形成平滑轨迹的正则化器。此外,将格拉斯曼混合与其他高效的序列建模模块(如状态空间模型、核化注意力或卷积模块)相结合,构建混合架构,也是一个有前景的研究方向,这可能有助于更好地平衡局部、全局和时间信息的处理 。
3. 几何不变性与可解释性提升
几何不变性是几何深度学习(Geometric Deep Learning)的核心概念之一,它指的是模型在特定变换群作用下保持其性质或输出的能力。在因果格拉斯曼架构中,几何不变性不仅是其数学优雅性的体现,更是其提升模型可解释性的根本机制。通过将模型的计算建立在具有内在几何不变性的格拉斯曼流形上,该架构为打开深度学习的“黑箱”提供了一把钥匙。
3.1 几何不变性的概念
几何不变性是数学和物理学中的一个基本概念,它描述的是在某些变换下保持不变的量或性质。在深度学习的语境下,几何不变性通常指的是模型对于输入数据的特定变换(如旋转、平移、缩放等)具有鲁棒性,即模型的输出不随这些变换而改变。例如,一个用于图像分类的卷积神经网络(CNN)具有平移不变性,因为无论物体在图像中的哪个位置,网络都能将其识别出来。这种不变性是通过网络结构(如卷积层和池化层)的设计来实现的。
3.1.1 定义:模型在特定变换下保持其性质或输出的特性
更形式化地,如果一个函数 f 对于一个变换群 G 中的元素 g 满足 f(ρ1(g)x) = ρ2(g)f(x),其中 ρ1 和 ρ2 分别是作用于输入空间和输出空间的群表示,那么我们称函数 f 是等变的(equivariant) 。如果输出空间的群表示是平凡的(即 ρ2(g) 是恒等变换),那么等变性就退化为不变性(invariance) ,即 f(ρ1(g)x) = f(x)。在因果格拉斯曼架构中,我们主要关注的是模型对于表示子空间的基变换所具有的不变性。这种不变性确保了模型关注的是子空间本身的几何属性,而不是用于表示它的特定基向量 。
几何不变性的重要性体现在多个方面。首先,它提高了模型的鲁棒性。通过强制模型学习对无关变换不变的特征,可以减少模型对数据特定形式的过拟合,从而提高其在真实世界数据上的泛化能力。其次,它提高了数据效率。模型不需要为每一种变换后的数据都学习一个新的表示,而是可以学习到一种更通用、更抽象的特征表示。最后,也是最重要的一点,它提高了模型的可解释性。当模型的行为受到明确的数学约束时,我们就更容易理解和分析其内部的决策逻辑。不变性为我们提供了一个分析模型的“锚点”,使得我们可以从几何和代数的角度来理解模型的表示 。
3.1.2 重要性:提高模型的稳健性、效率和可解释性
在因果格拉斯曼架构中,几何不变性的重要性得到了充分的体现。该架构的核心计算发生在格拉斯曼流形上,而这个流形本身就具有内在的几何不变性。具体来说,格拉斯曼流形 Gr(m, D) 上的点(即 D 维空间中的 m 维子空间)的定义是与基的选择无关的。这意味着,无论我们如何选择一组基向量来表示一个给定的子空间,这个子空间在格拉斯曼流形上的位置都是唯一的。这种内在的不变性为模型的稳健性和可解释性提供了坚实的基础 。
例如,在NLP任务中,一个句子或短语的含义不应该依赖于我们用来表示其中单词的特定嵌入向量。通过将标记对的关系建模为格拉斯曼流形上的子空间,因果格拉斯曼架构学习到的表示是内在的、与具体坐标系无关的。这使得模型对词嵌入空间中的微小扰动或基变换具有更强的鲁棒性。从可解释性的角度看,这种不变性使得我们可以用几何语言来描述模型的行为。我们不再纠结于单个向量的数值,而是可以讨论子空间的“朝向”、“大小”以及它们在流形上的“轨迹”。这些几何概念比高维张量中的数值更直观,也更容易与人类对语言的理解联系起来。因此,几何不变性不仅是因果格拉斯曼架构的一个数学特性,更是其设计理念的核心,是实现更透明、更可靠的人工智能的关键路径 。
3.2 Causal Grassmann中的几何不变性
因果格拉斯曼架构通过其核心的数学对象——格拉斯曼流形和普吕克坐标——将几何不变性深度融入到模型的设计中。这种设计使得模型的每一步计算都具有明确的几何意义,并且受到严格的数学约束,从而为可解释性提供了坚实的理论基础。
3.2.1 格拉斯曼流形的黎曼度量:在正交群作用下保持不变
格拉斯曼流形 Gr(n, p) 不仅是一个拓扑空间,还是一个黎曼流形,这意味着我们可以在其上定义距离、角度和曲率等几何概念。格拉斯曼流形上的黎曼度量是从其周围的欧几里得矩阵空间中诱导而来的。对于流形上的两个切向量 Δ1 和 Δ2,它们的内积被定义为 ⟨Δ1, Δ2⟩P = (1/2) Tr(Δ1^T Δ2),其中 Tr 表示矩阵的迹 。
这个度量的一个关键特性是它在正交群 O(n) 的作用下保持不变。也就是说,对于任何正交矩阵 Q ∈ O(n),我们有 ⟨QΔ1Q^T, QΔ2Q^T⟩QPQ^T = ⟨Δ1, Δ2⟩P。这意味着度量的值只依赖于子空间本身,而不依赖于用于表示该子空间的具体矩阵。这种内在的几何不变性是格拉斯曼流形的核心特性,也是因果格拉斯曼架构能够实现可解释性的根本原因。它确保了模型在比较两个子空间时,比较的是它们的几何属性,而不是它们的坐标表示。例如,模型可以计算两个子空间之间的测地线距离,这个距离是唯一的,并且具有明确的几何意义。通过分析模型在流形上的轨迹,我们可以量化模型在处理序列时的“移动”速度和“方向”,从而理解其动态行为 。
3.2.2 普吕克坐标的代数关系:提供明确的结构约束
普吕克坐标不仅提供了一种将子空间嵌入到射影空间的方法,它们还满足一组明确的代数关系,这些关系被称为 “普吕克关系式” 。这些关系式是二次的,它们定义了格拉斯曼流形作为射影空间中的一个代数簇。例如,对于 Gr(2, 4)(即4维空间中的2维子空间),其普吕克坐标 pij 满足方程 p12p34 - p13p24 + p14p_23 = 0。
这些代数关系为模型的行为提供了强大的结构约束。在因果格拉斯曼架构中,这意味着模型生成的所有普吕克向量都必须满足这些方程。这为模型的可解释性提供了另一个层面的支持。首先,这些关系式可以用来验证模型的输出是否在几何上是“有效”的。如果一个模型生成的普吕克向量不满足这些关系式,那么它在几何上是没有意义的。其次,这些关系式可以作为正则化项加入到模型的损失函数中,以引导模型学习更符合几何直觉的表示。例如,我们可以鼓励模型生成的普吕克向量在满足这些约束的同时,尽可能地接近某些预定义的、具有特定语义意义的子空间。
从可解释性的角度看,这些明确的代数关系使得我们可以利用代数几何的工具来分析和理解模型。我们可以研究模型学习到的普吕克向量在代数簇上的分布,或者分析不同任务或数据集对应的普吕克向量簇的几何性质。这与Transformer中注意力矩阵的无约束特性形成了鲜明对比,后者的分析通常缺乏这样坚实的数学基础。因此,普吕克坐标的代数关系为因果格拉斯曼架构的可解释性提供了从几何到代数的完整理论框架 。
3.3 可解释性提升路径
因果格拉斯曼架构通过引入几何不变性,为提升序列模型的可解释性提供了一条清晰的路径。这条路径的核心思想是将分析的重点从难以捉摸的高维张量转移到具有明确数学结构的流形轨迹上,并利用微分几何和代数几何的工具来定义和计算能够解释模型行为的全局不变量。
3.3.1 从张量提升到流形轨迹:将分析重点从高维张量转移到流形上的轨迹
Transformer模型的不可解释性在很大程度上源于其“张量提升”的核心机制。模型将序列表示提升到一个极高维的成对交互空间,并在那里进行操作。这个空间是如此之大,以至于我们很难找到一个简洁的方式来描述模型在其中的行为。我们面对的是一个不断演化的注意力张量云,而不是一条清晰的路径 。
因果格拉斯曼架构则提供了一种截然不同的视角。它将模型的计算核心从张量空间“降维”到了一个有限维的格拉斯曼流形上。在这个新的视角下,模型的行为不再是任意的张量操作,而是被解释为在格拉斯曼流形上的一条 “轨迹” 。序列中的每个标记对都对应着流形上的一个点,随着模型层数的增加,这些点在流形上移动,形成了一条轨迹。这条轨迹代表了模型在处理序列时,其内部表示的演化过程。这种从“张量云”到“流形轨迹”的转变是可解释性提升的关键一步。因为流形上的轨迹是一个几何对象,我们可以用几何的语言来描述和分析它。例如,我们可以计算轨迹的长度(代表了模型在处理序列时的“努力”程度)、曲率(代表了模型决策的“确定性”)或者它与特定语义子空间的接近程度。这些几何属性为我们理解模型的行为提供了直观而有力的工具 。
3.3.2 全局不变量的定义与计算:利用微分几何和代数几何工具进行分析
一旦我们将模型的行为视为流形上的轨迹,我们就可以利用微分几何和代数几何中的强大工具来定义和计算能够解释模型行为的全局不变量。这些不变量是模型行为的“指纹”,它们在不同的输入和任务中保持稳定,并且具有明确的数学和几何意义。
论文的作者提出了几种可能的全局不变量作为未来的研究方向 :
- 平均子空间(Averaged Subspaces) :我们可以计算模型在处理一个序列时,其内部子空间在格拉斯曼流形上的“平均位置”。这个平均子空间可以被认为是模型对该序列核心语义的“总结”。
- 曲率类度量(Curvature-like Measures) :我们可以分析模型轨迹在流形上的曲率。高曲率可能意味着模型在处理序列时遇到了复杂的、需要剧烈调整其内部表示的语义结构。
- 跨层稳定性统计量(Cross-layer Stability Statistics) :我们可以分析模型在不同层之间,其内部子空间变化的平滑程度。高稳定性可能意味着模型已经学习到了稳健的、层次化的特征表示。
这些全局不变量为我们提供了一个超越单个标记或注意力头的宏观视角来理解模型。通过比较不同模型或不同任务学习到的这些不变量,我们可以发现模型之间的共性和差异,从而更深入地理解深度学习的内在机制。例如,我们可以研究在情感分析任务中,表示积极和消极情感的句子对应的平均子空间在格拉斯曼流形上是否形成了清晰的聚类。这种基于几何和代数的分析方法,为可解释性研究开辟了一个全新的、充满潜力的领域。
3.3.3 跨层比较:普吕克向量在不同层之间的可比性
普吕克向量的一个关键优势是它们在不同层之间的直接可比性。由于普吕克坐标是格拉斯曼流形到射影空间的标准嵌入,任何一层计算出的普吕克向量都可以与任何其他层的普吕克向量进行有意义的比较。这种可比性为分析深度模型的层级特征学习提供了前所未有的便利。
在Transformer中,不同层的注意力头学习到的表示通常是异构的,很难直接进行比较。一个注意力头可能在第一层关注句法关系,在最后一层关注语义关系,而我们缺乏一个统一的框架来描述这种变化。相比之下,在因果格拉斯曼架构中,我们可以追踪一个特定的子空间(由其普吕克向量表示)是如何随着层数的增加而演化的。我们可以计算相邻层之间普吕克向量的“距离”(例如,在射影空间中的弦距离或测地线距离),从而量化模型在每一层对表示的“更新”幅度。我们可以绘制出这些距离随层数变化的曲线,从而直观地看到模型在哪些层进行了主要的“思考”和“推理”。
此外,我们还可以研究不同层学习到的普吕克向量在流形上的分布。例如,我们可以使用降维技术(如t-SNE或UMAP)将高维的普吕克向量可视化,并观察不同层的向量在二维平面上的分布模式。这种可视化可以帮助我们理解模型是如何在逐层处理中,将输入的序列信息从低级的语法特征逐渐抽象为高级的语义特征的。这种跨层的可比性,使得因果格拉斯曼架构不仅是一个强大的序列建模工具,更是一个研究深度学习内部工作原理的理想平台 。
4. 在NLP任务中的应用前景与挑战
因果格拉斯曼架构作为一种新兴的序列建模范式,为自然语言处理领域带来了新的可能性和研究方向。其在可解释性、计算效率和几何建模方面的独特优势,预示着它在多种NLP任务中具有广阔的应用前景。然而,作为一个尚处于早期研究阶段的架构,它也面临着诸多挑战和局限,需要学术界和工业界的共同努力来克服。
4.1 应用前景
因果格拉斯曼架构的应用前景主要体现在以下几个方面,它既可以作为现有模型的替代方案,也可以作为一种补充模块,以增强现有模型的性能。
4.1.1 语言建模:作为Transformer的替代或补充架构
语言建模是NLP领域最基础也是最重要的任务之一,它为各种下游任务提供了强大的预训练基础。目前,基于Transformer的语言模型(如GPT系列、BERT系列)在该领域占据主导地位。因果格拉斯曼架构的出现,为语言建模提供了一种全新的、不依赖于自注意力的替代方案。初步的实验结果表明,在中小规模的模型和数据集上,纯格拉斯曼语言模型已经能够与Transformer基线相媲美 。
未来的研究方向之一是探索如何进一步提升格拉斯曼语言模型的性能,使其能够在更大规模的数据集和模型上达到甚至超越Transformer的水平。这可能需要更精巧的架构设计,例如,探索更高维度的子空间(k > 2),或者设计更复杂的格拉斯曼流形上的演化规则。此外,将格拉斯曼混合层与Transformer的其他组件(如前馈网络、残差连接等)进行更深入的融合,构建混合架构,也是一个有前景的方向。例如,可以在Transformer的某些层中使用自注意力机制来捕捉全局依赖,而在其他层中使用格拉斯曼混合来建模局部几何关系,从而结合两者的优势。这种混合架构有望在保持Transformer强大表达能力的同时,引入格拉斯曼几何的结构化和可解释性优势。
4.1.2 自然语言推理(NLI):在特定任务上超越Transformer的潜力
自然语言推理(NLI)任务要求模型能够理解两个句子之间的逻辑关系(如蕴含、矛盾、中立)。这项任务对模型的语义理解和推理能力提出了很高的要求。在SNLI数据集上的实验结果显示,当一个因果格拉斯曼分类头被接在一个固定的预训练模型(DistilBERT)之上时,其性能略微优于传统的Transformer分类头 。
这个结果具有重要的启示。它表明,即使主干网络是传统的Transformer,在特定的下游任务中,引入显式的几何结构(通过格拉斯曼混合)也能够带来性能上的提升。这可能是因为NLI任务需要对句子对之间的细微语义差异进行建模,而格拉斯曼流形上的子空间表示恰好提供了一种有效的方式来捕捉这种“关系性”的信息。未来的研究可以进一步探索因果格拉斯曼架构在其他需要复杂推理的任务上的应用,例如问答系统、机器阅读理解、因果推理等。通过在这些任务上进行实验,我们可以更深入地理解格拉斯曼几何在多大程度上能够帮助模型进行更深层次的语义理解和逻辑推理。
4.1.3 长序列处理:线性复杂度使其在处理长文本时具有优势
处理长序列是Transformer架构面临的一个主要挑战,因为其自注意力机制的二次方计算复杂度 O(L²) 使得它在处理数千甚至数万个标记的序列时变得不切实际。因果格拉斯曼架构的线性复杂度 O(L) 使其在长序列处理方面具有天然的优势 。
这种优势使得因果格拉斯曼架构在许多需要处理长文本的应用场景中具有巨大的潜力,例如:
长文档摘要:需要对数千词的文档进行理解和概括。
对话系统:需要维护一个包含多轮对话历史的上下文。
代码生成:需要处理包含大量代码行的程序文件。
基因组学分析:需要分析长达数百万个碱基对的DNA序列。
在这些场景中,因果格拉斯曼架构不仅可以显著降低计算成本,还可能因为其局部性的建模假设而学习到更有效的长程依赖关系。未来的工作可以集中在将这些应用场景作为基准,系统地评估因果格拉斯曼架构在长序列处理上的性能和效率,并与现有的稀疏注意力机制进行全面的比较。
4.2 挑战与局限
尽管因果格拉斯曼架构展现出巨大的潜力,但它也面临着一系列挑战和局限,这些挑战限制了其当前的广泛应用,并指明了未来研究需要努力的方向。
| 挑战类别 | 具体描述 | 潜在解决方案/未来方向 |
|---|
| **模型成熟度** | 相较于Transformer,仍处于早期研究阶段,缺乏成熟的生态系统和预训练模型。 | 进行大规模预训练,探索多任务学习和微调策略,构建开源社区。 |
| **泛化能力** | 在更大规模数据集和更复杂任务上的表现有待验证,其“扩展定律”未知。 | 在Common Crawl等大规模语料库上进行预训练,在MMLU、Big-Bench等复杂推理基准上进行评估。 |
| **工程实现** | 将几何深度学习概念高效地集成到现有框架中是一个非-trivial的工程挑战,需要专门的GPU算子。 | 开发高效的几何深度学习库(如Geoopt的扩展),优化普吕克坐标计算和流形上的优化算法。 |
| **可解释性工具** | 缺乏专门的工具来可视化和分析格拉斯曼流形上的动态,研究门槛较高。 | 开发交互式流形浏览器、轨迹动画和不变量仪表盘等可视化与分析工具。 |
Table 2: Causal Grassmann架构面临的主要挑战与潜在解决方案
4.2.1 模型成熟度:相较于Transformer,仍处于早期研究阶段
Transformer架构自2017年提出以来,已经经过了多年的发展和优化,形成了一个庞大而成熟的生态系统。这包括大量的预训练模型、高效的工程实现(如各种深度学习框架中的优化)、丰富的微调策略以及广泛的社区支持。相比之下,因果格拉斯曼架构是一个非常新的概念,其相关的研究论文和开源实现都非常有限 。
这意味着,目前我们对该架构的理解还停留在比较初级的阶段。许多在Transformer领域已经成为标准实践的技术(如大规模预训练、多任务学习、知识蒸馏等)在因果格拉斯曼架构中的应用和效果还有待探索。此外,该架构的超参数(如降维后的维度 r、偏移量集合 W 的选择、子空间的维度 k 等)对模型性能的影响也缺乏系统性的研究。因此,要将因果格拉斯曼架构发展成为一个能够与Transformer相抗衡的成熟范式,还需要大量的理论研究和工程实践工作。
4.2.2 泛化能力:在更大规模数据集和更复杂任务上的表现有待验证
目前关于因果格拉斯曼架构的实验主要是在中小规模的数据集(如Wikitext-2, SNLI)和模型(13-18M参数)上进行的。虽然这些初步结果令人鼓舞,但它们能否推广到更大、更复杂的场景还是一个未知数。例如,在包含数千亿词的大规模语料库上进行预训练时,格拉斯曼语言模型是否还能保持其竞争力?在面对需要复杂世界知识和多步推理的基准测试(如MMLU, Big-Bench)时,该架构的表现如何?
论文的作者也指出,他们目前的模型在语言建模任务上并未超越Transformer,这可能与设计的简单性和缺乏大规模调优有关 。因此,一个关键的挑战是进行大规模的实验,以验证因果格拉斯曼架构的 “扩展定律”(scaling laws) 。这需要强大的计算资源和精心的实验设计。只有在更大规模和更复杂的任务上证明了其有效性和鲁棒性,因果格拉斯曼架构才能真正被认为是Transformer的一个有力竞争者。
4.2.3 工程实现:将几何深度学习概念高效地集成到现有框架中
将几何深度学习的概念(如格拉斯曼流形、普吕克坐标)高效地集成到现有的深度学习框架(如PyTorch, TensorFlow)中是一个非-trivial的工程挑战。虽然理论上因果格拉斯曼混合层的复杂度是线性的,但要将这个理论优势在实践中发挥出来,需要专门的GPU算子和优化的计算图。
例如,计算普吕克坐标涉及到大量的2x2子行列式计算,如何将这些计算并行化以充分利用GPU的计算能力是一个需要解决的问题。此外,格拉斯曼流形上的优化(如计算测地线、指数映射等)也需要专门的数值算法。目前,虽然已经有一些几何深度学习的库(如Geoopt),但它们对格拉斯曼流形的支持可能还不够完善,或者效率不够高。因此,开发高效、易用的格拉斯曼深度学习工具箱是推动该领域发展的关键一步。这需要计算机科学家和数学家的紧密合作,将抽象的数学概念转化为高效的、可落地的工程实现 。
4.2.4 可解释性工具:需要开发专门的工具来可视化和分析格拉斯曼流形上的动态
虽然因果格拉斯曼架构在理论上为可解释性提供了坚实的基础,但要将这些理论优势转化为实际的分析能力,还需要开发专门的工具来可视化和分析格拉斯曼流形上的动态。目前,我们缺乏能够直观展示高维格拉斯曼流形上点和轨迹的工具。
未来的工作需要开发新的可视化技术,例如:
交互式流形浏览器:允许研究者在格拉斯曼流形上“漫游”,查看不同子空间的位置和关系。
轨迹动画:动态展示模型在处理序列时,其内部子空间在流形上的演化过程。
- 不变量仪表盘:实时计算和展示各种全局不变量(如平均子空间、曲率等)的值,并允许研究者进行交互式探索。
此外,还需要开发新的分析工具,例如,用于发现普吕克向量簇的聚类算法,或者用于比较不同模型学习到的几何结构的统计检验方法。这些工具的开发将大大降低研究门槛,使得更多的研究者能够利用几何方法来分析和理解他们的模型。这将是连接几何深度学习理论与可解释性实践的重要桥梁 。