执行摘要
大语言模型困惑度的核心价值与应用概览
核心洞察
困惑度(Perplexity, PPL)是衡量大语言模型预测能力的核心指标,本质上是模型面对文本序列时"惊讶程度"的量化,数学上等于交叉熵的指数(PPL = 2^H)。它通过几何平均条件概率的倒数计算,反映模型每一步预测面临的有效选择分支数。
技术实现
现代LLM通过实时追踪Token级对数概率(Logprobs)实现增量式困惑度计算
应用于早期停止、质量监控和自适应推理(如CAR框架)
由于自回归架构的信息瓶颈,模型无法通过简单Prompt直接输出自身困惑度
理论关联
需借助Verbalized Confidence等间接方法或外部计算
困惑度与信息论中的熵、交叉熵、KL散度存在严格数学等价关系
是评估模型校准、检测幻觉和优化推理效率的关键工具
理论基础与数学定义
从信息论视角深入理解困惑度的本质
核心概念与直观解释
不确定性度量
量化语言模型在面对文本序列时的"惊讶程度"或不确定性水平。困惑度为100意味着模型在预测每个Token时,相当于面对100个等概率选择的决策空间。
分支因子
将模型的不确定性量化为等效的选择空间大小。GPT-4在标准英语文本上的困惑度维持在15-20之间,表明每次预测相当于从15-20个等概率选项中选择。
几何平均本质
困惑度本质上是序列概率几何平均的倒数,对概率分布中的极端值具有高度敏感性,能够严厉惩罚模型在任何一个位置上的严重预测失误。
数学定义与计算公式
序列联合概率的链式法则分解
P(w₁, w₂, ..., wₙ) = ∏ᵢ₌₁ⁿ P(wᵢ | w₁, w₂, ..., wᵢ₋₁)
这一分解反映了语言模型的自回归本质:每个Token的生成仅依赖于其左侧的上下文。在Transformer架构中,这种条件依赖通过自注意力机制实现。
平均负对数似然(NLL)计算
NLL = -¹/ₙ ∑ᵢ₌₁ⁿ log P(wᵢ | w₁, ..., wᵢ₋₁)
为避免数值下溢问题并简化计算,实践中通常采用对数形式。该公式将概率乘积转换为对数概率求和,显著提升了数值稳定性。
指数转换与困惑度标准化
Perplexity = exp(NLL) = exp(-¹/ₙ ∑ᵢ₌₁ⁿ log P(wᵢ | w<ᵢ))
这一指数转换将平均"惊讶度"转换回等效的"选择分支数"。最小化困惑度等价于最大化训练数据的似然概率,这正是语言模型训练的核心目标。
与信息论熵的关系
困惑度与交叉熵的指数关系
Perplexity = 2H(p,q)
困惑度可简洁地表示为交叉熵的指数。这一关系表明,最小化困惑度等价于最小化交叉熵损失,为困惑度提供了信息论基础的严谨性。
与条件熵的数学等价性
Perplexity = 2H(Y|X)
在序列建模语境下,困惑度与条件熵紧密相关。条件熵量化了在给定历史条件下,下一个Token的剩余不确定性。
通用计算方法与工程实现
从理论到实践的完整计算流程
基于Token概率的标准计算流程
文本分词与编码
使用与模型训练时完全相同的分词器(Tokenizer),将原始文本转换为Token ID序列。
前向传播获取Logprobs
通过模型前向传播获取每个位置的条件概率分布,提取目标Token的对数概率。
logprobs = log_softmax(logits)
累加平均与指数运算
对所有位置的负对数似然求平均,然后应用指数函数得到最终的困惑度值。
长序列处理策略
滑动窗口方法(Sliding Window)
对于超出模型最大上下文长度的长文档,将序列分割为重叠的固定长度片段,每个片段独立计算困惑度后平均。
实验数据
在WikiText-2数据集上,使用步长为512的滑动窗口策略相比朴素分块方法,困惑度从19.64降至16.53,改进幅度达15.8%。
开源工具与框架实现

Hugging Face Transformers
标准化实现方案
对于支持
labels参数的因果语言模型,可直接利用模型的内置损失计算功能。
Evaluate库
标准化评估流程
自动处理设备分配、混合精度计算、批量处理以及不同模型的特定需求,支持分布式评估。
推理过程中的实时计算
动态监控与智能决策机制
实时计算原理
概率流追踪
在自回归生成过程中,捕获每个步骤的条件概率分布,而非仅关注最终生成文本。实时困惑度基于这些分布中实际选中Token的概率计算。
增量式更新
维护运行中的对数概率和与Token计数,每生成新Token立即更新困惑度。内存效率高(O(1)空间复杂度),适用于流式生成场景。
KV缓存优化
与KV缓存机制协同工作,复用缓存的隐藏状态,仅需计算最新Token的logits,将每步推理复杂度从O(t²)降至O(t)。
API层面的实时获取
OpenAI API的logprobs参数配置
现代大语言模型API提供了
logprobs参数,允许开发者在生成文本的同时获取Token级别的概率信息。
返回结构包含
- • token: 实际生成的Token字符串
- • logprob: 该Token的对数概率
- • bytes: Token的ASCII编码
- • top_logprobs: 最可能的k个候选Token
流式响应中的概率提取
流式传输API允许在生成过程中逐步接收Token,结合
logprobs参数支持真正的实时困惑度监控。
应用场景与决策机制
CAR框架:基于困惑度的自适应推理
字节跳动与复旦大学联合提出的CAR框架通过实时评估模型对短答案的困惑度,智能判断是否需要触发详细的长形式推理过程。
CAR框架性能表现
| 模型 | 方法 | 平均准确率 | Token使用量 | 准确率提升 | Token减少 |
|---|---|---|---|---|---|
| Qwen2.5-7B | 纯长文本推理 | 75.0% | 基准值 | - | - |
| Qwen2.5-7B | CAR框架 | 81.1% | 减少21.4% | +6.9% | 21.4% |
| Llama3.1-8B | 纯长文本推理 | 70.8% | 基准值 | - | - |
| Llama3.1-8B | CAR框架 | 74.9% | 减少39.0% | +5.5% | 39.0% |
通过Prompt获取模型自身困惑度
间接方法与外部计算方案
直接Prompt方法的局限性
内部概率不可访问
困惑度计算依赖完整概率分布,而标准API仅返回生成文本,不暴露底层概率信息。
信息瓶颈
自回归架构的因果特性构成信息瓶颈,模型无法"回忆"已生成内容的历史概率状态。
API功能边界
当前主流API不暴露完整logits向量、中间层隐藏状态或注意力权重矩阵。
基于置信度估计的间接方法
口语化置信度表达(Verbalized Confidence)
通过特定Prompt引导模型评估其答案的正确性概率。研究表明,这种口语化置信度与真实准确率存在正相关,但相关性较弱(通常0.3-0.5)。
示例Prompt
自我反思机制(Self-Reflection)
要求模型检查其推理过程并识别潜在错误。虽然这些方法在某些基准测试上显示出与准确率的正相关,但它们显著增加了计算成本。
P(True)方法
评估生成内容正确的概率
多轮采样
多次询问并取平均值
内省不确定性
识别推理缺陷并调整置信度
基于外部计算的Prompt辅助方案
Token级概率分布
利用API的logprobs功能,外部系统计算生成内容的困惑度,模型负责生成便于评估的格式。
ppl = calculate_perplexity(logits)
RAG知识源置信度
在检索增强生成系统中,结合困惑度与检索文档的一致性评估回答可靠性。
confidence = align_with_retrieval
代理模型校准
使用较小的开源模型作为代理,估计闭源模型的困惑度,形成"模型监督模型"的架构。
proxy_ppl = proxy_model(text)
困惑度与熵的深层关系
信息论视角下的理论关联与分析
交叉熵与困惑度的数学等价
严格数学对应关系
Perplexity = 2H(p,q)
理论基础:交叉熵H(p,q)衡量使用分布q编码来自分布p的数据所需的平均比特数
优化等价:最小化困惑度等价于最小化交叉熵损失
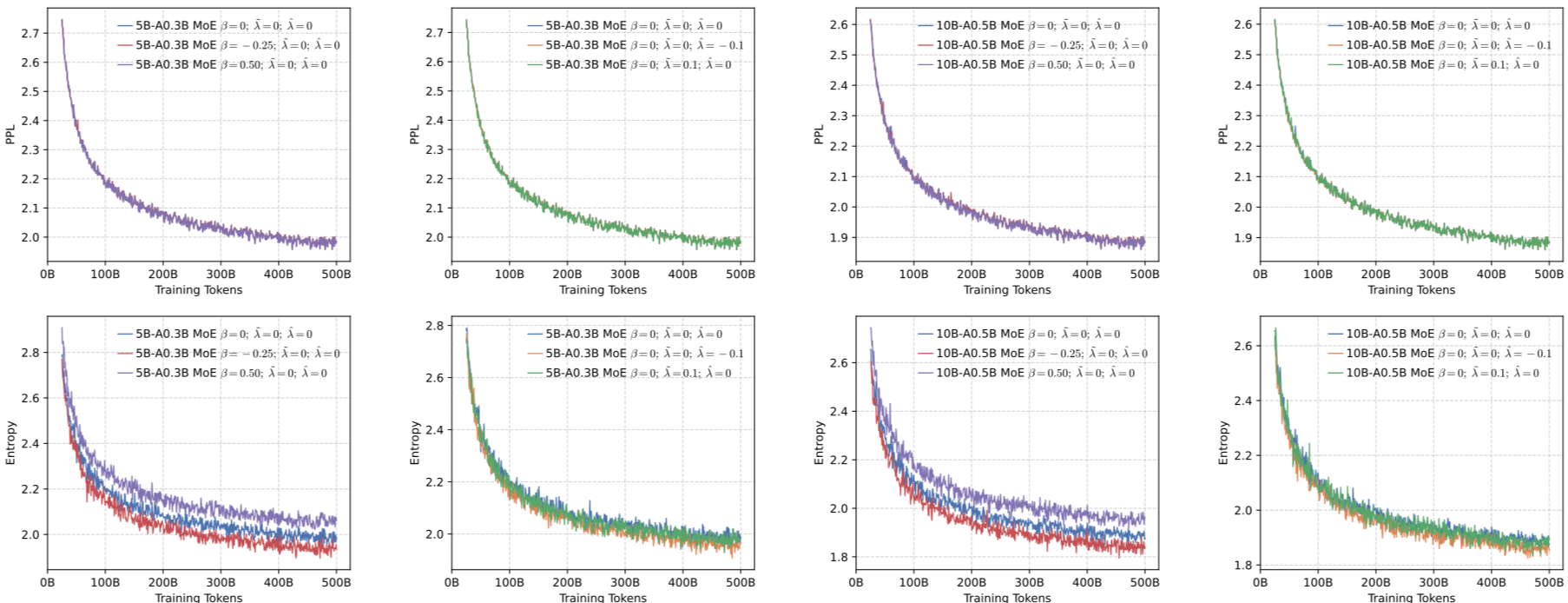
模型训练中的困惑度下降曲线
初期快速下降
从数百降至数十,学习基本语法和常见词汇搭配
中期缓慢下降
数十降至十几,学习语义关联和领域特定知识
后期趋于平稳
开始过拟合,需触发早停机制
条件熵与序列建模
条件熵的体现
条件熵H(Y|X)量化了在给定上下文X的条件下,目标变量Y的不确定性。在语言模型中,这对应于给定前文w<ᵢ时,下一个词元wᵢ的不确定性。
上下文依赖示例
渐进困惑度理论
对于无限长序列,渐进困惑度与熵率的关系由Shannon-McMillan-Breiman定理描述:当序列长度N→∞时,困惑度收敛于2H(X)。
limN→∞ Perplexity = 2H∞
信息论视角下的模型分析
困惑度作为压缩效率指标
从数据压缩视角,困惑度直接对应于无损压缩的理论极限。困惑度越低,模型对数据的压缩效率越高。
压缩效率对比
不确定性校准与模型可靠性
困惑度与模型校准密切相关。一个完美校准的模型,其预测概率应准确反映事件的真实发生频率。困惑度对高置信度错误惩罚极重,使其成为可靠性的重要指标。
过度自信
预测概率高于实际准确率
信心不足
预测概率低于实际准确率
完美校准
预测概率等于实际准确率
困惑度在LLM评估中的应用
从基础评估到前沿研究的完整应用场景
模型性能基准测试
困惑度作为通用评估指标
困惑度是语言模型最基础、最通用的内在评估指标,广泛应用于模型开发、选型和迭代优化。与外在评估相比,困惑度计算无需标注数据,成本低廉且可扩展。
域内与域外困惑度分析
模型在训练分布(In-domain)和未见过领域(Out-of-domain)的困惑度差异揭示了泛化能力。理想模型应保持困惑度稳定。
能力地图
通过系统评估多个领域的困惑度(新闻、科学、小说、代码),可绘制模型的"能力地图",识别强项和弱项。
不确定性量化与校准
置信度校准技术
完美校准的模型在报告80%置信度时,应有80%的回答正确。通过绘制可靠性图表,可以可视化不同困惑度区间内的实际准确率。
温度缩放
调整Softmax温度参数
ECE计算
预期校准误差量化
幻觉检测与困惑度阈值
困惑度在幻觉检测中的应用基于观察:模型对其幻觉内容的置信度通常较低(表现为较高的困惑度)。然而,这种关联并非绝对,存在"自信的错误"现象。
困惑度异常
突然飙升
检索一致性
RAG场景
自我一致性
多次采样
模式识别
特定幻觉
高级应用与前沿研究
CAR框架:基于困惑度的自适应推理
CAR框架的技术实现依赖于对困惑度与答案正确性关系的统计建模,假设正确与错误短答案的PPL分布分别服从高斯分布,通过贝叶斯定理计算后验概率进行决策。
核心创新
打破了"长文本推理必然性能更好"的固有认知,为大模型推理提供了更灵活高效的解决方案。
统计建模
高斯分布假设 + 贝叶斯定理
动态路由
短答案 vs 长推理智能选择
性能提升
准确率+6.9%,Token-21.4%
PAQ框架:Prompt-Adaptive Quantization
Algoverse AI Research提出的PAQ框架训练了一个轻量级的BERT路由器,使用困惑度引导监督来为每个输入提示选择最小的足够量化级别(2、4、8或16位)。
核心假设
不同复杂度的提示对数值精度的需求不同:简单输入用低精度,复杂查询需高精度。
| 量化级别 | 使用率 | 延迟优化 |
|---|---|---|
| 2位模型 | 41.7% | 最快 |
| 4位模型 | 30.0% | 快速 |
| 8位模型 | 10.2% | 中等 |
| 16位模型 | 18.0% | 基准 |
性能提升:平均延迟从24.5秒降低到8.3秒(减少66%)
SPIRIT:Stepwise Perplexity-Guided Refinement
通过计算每个推理步骤对整体困惑度的贡献,识别并移除或合并不重要的步骤,从而优化推理链的效率。实验在Algebra-Linear-1d Task和Number-Base-Conversion Task上验证了困惑度引导的步骤选择能够显著提高少样本CoT的预测准确性。
SPIRIT-FS
少样本CoT场景优化
SPIRIT-FT
微调场景优化

