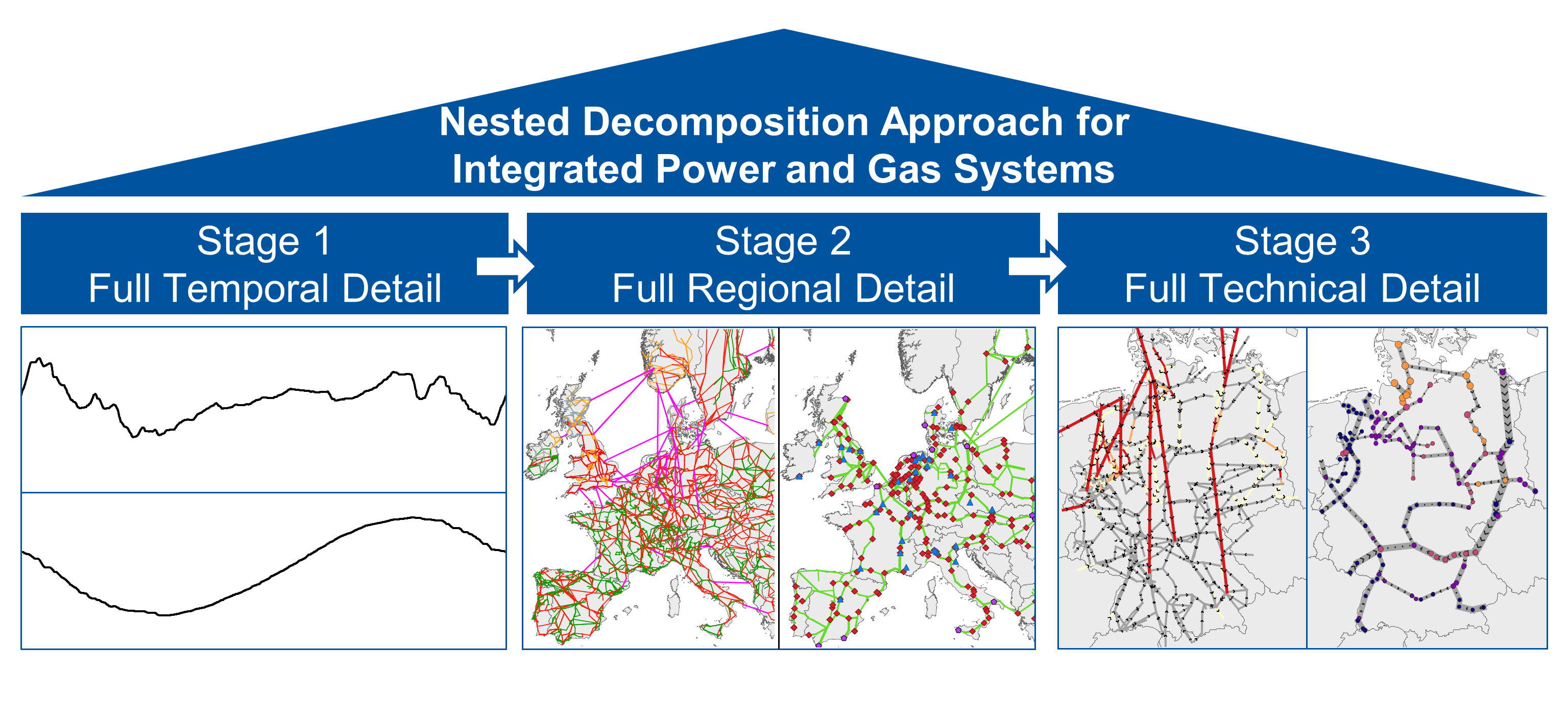
The Nested Learning Paradigm
A foundational shift that dissolves the traditional distinction between model architecture and optimization algorithms, revealing models as dynamic systems of nested, multi-level optimization problems.
Unified Architecture
NL treats model architecture and optimization as a single, integrated system where components operate at different timescales.
Context Flow
Models learn by compressing internal context flows, turning each optimization level into an associative memory module.
Multi-Timescale
Neuroscientifically inspired approach with different components updating at varying frequencies for optimal learning.
Core Philosophy
The central tenet of Nested Learning is the unification of model architecture and optimization algorithms, which have traditionally been treated as distinct entities in machine learning [1] [2]. This unification is achieved by re-conceptualizing a neural network not as a static structure of parameters, but as a collection of interconnected optimization processes, each operating at its own frequency and with its own independent "context flow" [3].
Explaining In-Context Learning
The Nested Learning framework offers a compelling explanation for the phenomenon of in-context learning (ICL), where large language models can learn to perform new tasks based solely on a few examples provided in the input prompt, without any explicit gradient-based training [3]. According to NL, ICL is not a magical emergent property but a natural consequence of the model's nested optimization structure.
Deep Optimizers: A New Class of Learning Algorithms
Reimagining standard optimizers like Adam and SGD with Momentum as associative memory modules that learn to compress gradients, enabling more powerful and adaptive optimization.
Traditional Optimizers
Deep Optimizers
- Learnable memory modules
- Gradient compression systems
- Frequency-aware updates
Deep Optimizers transform traditional gradient-based updates into associative memory modules that learn to compress and optimize gradient information across multiple timescales.
Reimagining Optimization
The core idea behind Deep Optimizers is to view the optimization process through the lens of associative memory [4]. In this framework, the optimizer is not just a set of rules for updating parameters; it is a memory system that stores and retrieves information about the gradients it has seen in the past. When a new gradient is received, the optimizer uses its memory to compute an update that is informed by the history of previous gradients.
Deep Momentum Gradient Descent
One of the proposed optimizers is Deep Momentum Gradient Descent, which uses an MLP to store and process the gradient history [5]. Instead of using a simple exponential moving average to compute the momentum term, this optimizer uses an MLP to learn a more complex function of the past gradients. This allows the optimizer to learn more sophisticated patterns in the gradient sequence, such as periodicities or long-range dependencies [6].
The HOPE Architecture: A Self-Modifying System
HOPE (Hierarchical Optimization with Parameter Evolution) demonstrates the practical potential of Nested Learning through a self-modifying sequence model that learns to adapt its own learning algorithm.
Self-Modifying
Learns to predict optimal parameter updates based on current context and loss function.
Multi-Timescale
Continuum Memory System manages information across different temporal scales.
Unbounded Levels
Achieves infinite nested learning loops for recursive self-improvement.
Continuum Memory System
The Continuum Memory System (CMS) is another key innovation in the HOPE architecture [4]. It is a new formulation for memory systems that generalizes the traditional view of long-term and short-term memory. Instead of having a fixed number of memory stores, CMS provides a continuous spectrum of memory modules, each with its own update frequency and retention characteristics [6].
Self-Referential Optimization
Self-referential optimization is a key concept in the HOPE architecture and a direct consequence of the Nested Learning paradigm [5]. It refers to the ability of the model to modify its own learning rules during inference, allowing it to adapt to new information and to improve its performance over time. By enabling the model to learn how to learn, self-referential optimization opens up the possibility of creating truly intelligent systems that can continually evolve and improve.
Empirical Validation and Performance
Comprehensive experimental results demonstrate HOPE's superior performance across language modeling, continual learning, and long-context reasoning tasks.
Performance Summary
| Task Category | Benchmark | Key Finding | Source |
|---|---|---|---|
| Language Modeling | WikiText-103, LAMBADA | Lower perplexity than Transformers and recurrent models | [7] |
| Long-Context Reasoning | "Hunting" task, Babi tasks | Superior performance in long-range dependencies | [7] |
| Continual Learning | Permuted MNIST, Split CIFAR-100 | Minimal catastrophic forgetting across task sequences | [7] |
Key Achievements
-
Superior Language UnderstandingLower perplexity than state-of-the-art models
-
Enhanced Memory ManagementBetter long-context reasoning capabilities
-
Continual Learning BreakthroughMinimal catastrophic forgetting observed
HOPE's Continuum Memory System enables fine-grained control over memory retention and forgetting, crucial for continual learning applications.
Breakthrough in Continual Learning
The results on continual learning benchmarks show that HOPE is able to achieve a breakthrough in performance, with minimal catastrophic forgetting. This is a major contribution of the paper, as it addresses one of the most persistent challenges in artificial intelligence [8]. The ability of HOPE to learn continuously without forgetting previously acquired knowledge is a direct result of its nested optimization structure and its Continuum Memory System.
Potential Impact and Future Research
Nested Learning offers a path towards addressing fundamental AI challenges, with implications for personalized AI, recommender systems, lifelong learning agents, and the development of Artificial General Intelligence.
Fundamental AI Challenges
- Overcoming catastrophic forgetting in neural networks
- Path towards more robust and adaptive AI systems
- Implications for Artificial General Intelligence
Applications & Extensions
- Personalized AI companions and adaptive interfaces
- Advanced recommender systems with real-time personalization
- Lifelong learning agents and robotics
Future Research Directions
Scaling HOPE
Scaling to larger and more complex models while managing computational costs
Theoretical Analysis
Deeper mathematical analysis of Nested Learning dynamics and convergence properties
Integration
Integration with other AI paradigms like Retrieval-Augmented Generation
Open Questions
The Nested Learning paper also raises a number of open questions and outlines several directions for future work. These include scaling the HOPE architecture to larger and more complex models, conducting a more thorough theoretical analysis of the Nested Learning dynamics, and integrating the framework with other AI paradigms [9].
"The Nested Learning paradigm could have important implications for the development of Artificial General Intelligence, providing a framework for designing models that can learn and adapt in a more human-like manner."
