гҖҠAttention Is All You NeedгҖӢзҡ„L2е№іж–№еӨҚжқӮеәҰдёҺвҖңй»‘зӣ’вҖқй—®йўҳпјҡжӣҝд»Јж–№жЎҲж·ұеәҰз ”з©¶еҸҠж–°жЁЎеһӢеҲҶжһҗ
1. TransformerжЁЎеһӢзҡ„ж ёеҝғжҢ‘жҲҳпјҡL2е№іж–№еӨҚжқӮеәҰдёҺвҖңй»‘зӣ’вҖқй—®йўҳ
иҮӘ2017е№ҙVaswaniзӯүдәәеҸ‘иЎЁејҖеҲӣжҖ§и®әж–ҮгҖҠAttention Is All You NeedгҖӢд»ҘжқҘпјҢеҹәдәҺTransformerжһ¶жһ„зҡ„жЁЎеһӢе·ІжҲҗдёәиҮӘ然иҜӯиЁҖеӨ„зҗҶпјҲNLPпјүд№ғиҮіж•ҙдёӘж·ұеәҰеӯҰд№ йўҶеҹҹзҡ„еҹәзҹі гҖӮе…¶ж ёеҝғеҲӣж–°вҖ”вҖ”иҮӘжіЁж„ҸеҠӣжңәеҲ¶пјҲSelf-AttentionпјүпјҢйҖҡиҝҮе…Ғи®ёеәҸеҲ—дёӯзҡ„жҜҸдёӘе…ғзҙ зӣҙжҺҘе…іжіЁе…¶д»–жүҖжңүе…ғзҙ пјҢеҪ»еә•ж”№еҸҳдәҶеәҸеҲ—ж•°жҚ®зҡ„еӨ„зҗҶж–№ејҸпјҢжңүж•Ҳи§ЈеҶідәҶдј з»ҹеҫӘзҺҜзҘһз»ҸзҪ‘з»ңпјҲRNNпјүеңЁеӨ„зҗҶй•ҝи·қзҰ»дҫқиө–пјҲLong-Range Dependenciesпјүж—¶зҡ„瓶йўҲпјҢ并жһҒеӨ§ең°жҸҗеҚҮдәҶжЁЎеһӢзҡ„并иЎҢи®Ўз®—иғҪеҠӣ гҖӮ然иҖҢпјҢйҡҸзқҖжЁЎеһӢ规模зҡ„жҢҮж•°зә§еўһй•ҝе’Ңеә”з”ЁеңәжҷҜзҡ„дёҚж–ӯжӢ“е®ҪпјҢTransformerжһ¶жһ„еӣәжңүзҡ„дёӨдёӘж ёеҝғжҢ‘жҲҳд№ҹж—ҘзӣҠеҮёжҳҫпјҡдёҖжҳҜиҮӘжіЁж„ҸеҠӣжңәеҲ¶еёҰжқҘзҡ„дәҢж¬Ўж–№и®Ўз®—еӨҚжқӮеәҰпјҲL2 Complexityпјү пјҢеҚіO(nВІ) пјҢиҝҷдёҘйҮҚйҷҗеҲ¶дәҶжЁЎеһӢеңЁеӨ„зҗҶй•ҝеәҸеҲ—д»»еҠЎж—¶зҡ„ж•ҲзҺҮе’ҢеҸҜиЎҢжҖ§пјӣдәҢжҳҜе…¶ вҖңй»‘зӣ’вҖқпјҲBlack Boxпјүзү№жҖ§пјҢеҚіжЁЎеһӢеҶ…йғЁеҶізӯ–иҝҮзЁӢзҡ„й«ҳеәҰеӨҚжқӮжҖ§е’ҢдёҚеҸҜи§ЈйҮҠжҖ§пјҢиҝҷз»ҷжЁЎеһӢзҡ„и°ғиҜ•гҖҒдјҳеҢ–д»ҘеҸҠеңЁе…ій”®йўҶеҹҹзҡ„еә”з”ЁеёҰжқҘдәҶе·ЁеӨ§йҡңзўҚгҖӮиҝҷдёӨдёӘй—®йўҳдёҚд»…жҳҜеҪ“еүҚз ”з©¶зҡ„зғӯзӮ№пјҢд№ҹеӮ¬з”ҹдәҶеӨ§йҮҸж—ЁеңЁдјҳеҢ–жҲ–жӣҝд»Јж ҮеҮҶTransformerжһ¶жһ„зҡ„еҲӣж–°е·ҘдҪңгҖӮ
1.1 L2е№іж–№еӨҚжқӮеәҰй—®йўҳ
L2е№іж–№еӨҚжқӮеәҰй—®йўҳпјҢжӣҙеҮҶзЎ®ең°иҜҙжҳҜдәҢж¬Ўж–№еӨҚжқӮеәҰй—®йўҳпјҢжҳҜTransformerжһ¶жһ„жңҖи‘—еҗҚдё”жңҖе…·жҢ‘жҲҳжҖ§зҡ„瓶йўҲгҖӮе®ғжәҗдәҺиҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„ж ёеҝғи®Ўз®—иҝҮзЁӢпјҢеҚіи®Ўз®—еәҸеҲ—дёӯжүҖжңүtokenеҜ№д№Ӣй—ҙзҡ„зӣёдә’е…ізі»гҖӮиҷҪ然иҝҷз§Қе…ЁеұҖж„ҹеҸ—йҮҺжҳҜTransformerејәеӨ§жҖ§иғҪзҡ„е…ій”®пјҢдҪҶе…¶и®Ўз®—е’ҢеҶ…еӯҳејҖй”ҖйҡҸзқҖеәҸеҲ—й•ҝеәҰзҡ„еўһеҠ иҖҢе‘ҲдәҢж¬Ўж–№еўһй•ҝпјҢиҝҷдҪҝеҫ—еӨ„зҗҶй•ҝж–ҮжЎЈгҖҒй•ҝи§Ҷйў‘гҖҒеҹәеӣ з»„еәҸеҲ—зӯүи¶…й•ҝеәҸеҲ—д»»еҠЎеҸҳеҫ—ејӮеёёеӣ°йҡҫе’ҢжҳӮиҙө гҖӮи®ёеӨҡеӨ§еһӢTransformerжЁЎеһӢеҸӘиғҪеңЁеӨ§еһӢе·Ҙдёҡз ”з©¶е®һйӘҢе®Өдёӯи®ӯз»ғпјҢе…¶е·ЁеӨ§зҡ„еҶ…еӯҳйңҖжұӮз”ҡиҮідҪҝеҫ—еңЁеҚ•дёӘGPUдёҠиҝӣиЎҢеҫ®и°ғйғҪжҲҗдёәдёҚеҸҜиғҪпјҢиҝҷжһҒеӨ§ең°йҷҗеҲ¶дәҶз ”з©¶зҡ„жҷ®еҸҠе’Ңж·ұе…Ҙ гҖӮ
1.1.1 иҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„计算瓶йўҲ
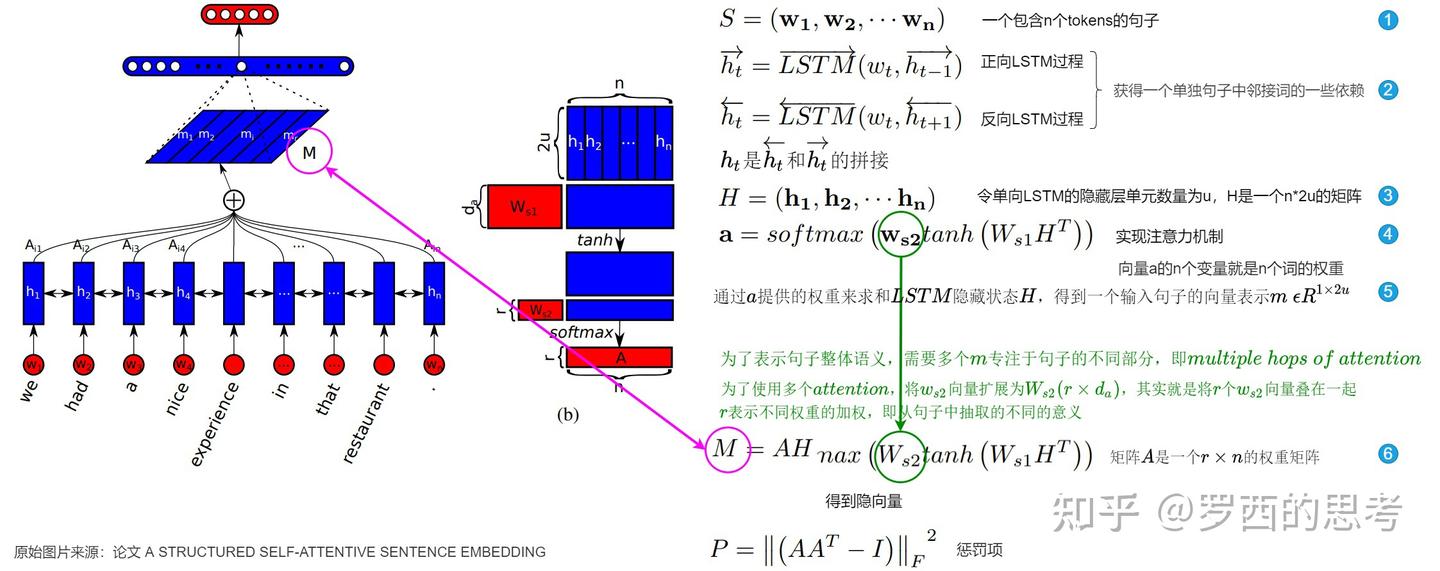
иҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„计算瓶йўҲдё»иҰҒдҪ“зҺ°еңЁе…¶ж ёеҝғзҡ„вҖңжҹҘиҜў-й”®-еҖјвҖқпјҲQuery-Key-Value, QKVпјүжЁЎеһӢдёҠгҖӮеҜ№дәҺдёҖдёӘй•ҝеәҰдёәnзҡ„иҫ“е…ҘеәҸеҲ—пјҢжҜҸдёӘtokenйғҪдјҡиў«зәҝжҖ§жҳ е°„дёәжҹҘиҜўеҗ‘йҮҸQгҖҒй”®еҗ‘йҮҸKе’ҢеҖјеҗ‘йҮҸVгҖӮиҮӘжіЁж„ҸеҠӣзҡ„иҫ“еҮәжҳҜйҖҡиҝҮи®Ўз®—QдёҺжүҖжңүKзҡ„зӮ№з§ҜпјҢеҫ—еҲ°жіЁж„ҸеҠӣеҲҶж•°зҹ©йҳөпјҢеҶҚз»ҸиҝҮsoftmaxеҪ’дёҖеҢ–еҗҺдёҺVиҝӣиЎҢеҠ жқғжұӮе’Ңеҫ—еҲ°зҡ„ гҖӮиҝҷдёӘиҝҮзЁӢзҡ„ж•°еӯҰиЎЁиҫҫејҸдёә Attention(Q, K, V) = softmax(QK^T / sqrt(d_k))VгҖӮе…¶дёӯпјҢжңҖе…ій”®зҡ„и®Ўз®—жӯҘйӘӨжҳҜз”ҹжҲҗдёҖдёӘnГ—nзҡ„жіЁж„ҸеҠӣеҲҶж•°зҹ©йҳөпјҢиҜҘзҹ©йҳөзҡ„жҜҸдёӘе…ғзҙ д»ЈиЎЁдәҶеәҸеҲ—дёӯдёӨдёӘдҪҚзҪ®д№Ӣй—ҙзҡ„зӣёе…іжҖ§жқғйҮҚгҖӮиҝҷдёӘзҹ©йҳөзҡ„и®Ўз®—е’ҢеӯҳеӮЁжҳҜеҜјиҮҙдәҢж¬Ўж–№еӨҚжқӮеәҰзҡ„ж №жң¬еҺҹеӣ гҖӮеҪ“еәҸеҲ—й•ҝеәҰnд»ҺеҮ зҷҫеўһеҠ еҲ°еҮ еҚғз”ҡиҮідёҠдёҮж—¶пјҢи®Ўз®—йҮҸе’ҢеҶ…еӯҳеҚ з”ЁдјҡжҖҘеү§иҶЁиғҖпјҢжҲҗдёәж•ҙдёӘжЁЎеһӢи®ӯз»ғе’ҢжҺЁзҗҶиҝҮзЁӢдёӯзҡ„дё»иҰҒ瓶йўҲ гҖӮ
1.1.2 еӨҚжқӮеәҰеҲҶжһҗпјҡO(nВІd)зҡ„ж—¶й—ҙдёҺз©әй—ҙеӨҚжқӮеәҰ
еҜ№иҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„еӨҚжқӮеәҰиҝӣиЎҢзІҫзЎ®еҲҶжһҗпјҢеҸҜд»ҘжҸӯзӨә其计算瓶йўҲзҡ„е…·дҪ“жқҘжәҗгҖӮеҒҮи®ҫиҫ“е…ҘеәҸеҲ—й•ҝеәҰдёәnпјҢtokenзҡ„еөҢе…Ҙз»ҙеәҰдёәdпјҢеӨҡеӨҙжіЁж„ҸеҠӣжңәеҲ¶зҡ„еӨҙж•°дёәhпјҢжҜҸдёӘеӨҙзҡ„з»ҙеәҰдёәdk = d/hгҖӮ
ж—¶й—ҙеӨҚжқӮеәҰеҲҶжһҗпјҡ
иҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„и®Ўз®—дё»иҰҒеҢ…еҗ«д»ҘдёӢеҮ дёӘжӯҘйӘӨ пјҡ
- QKбөҖзҹ©йҳөд№ҳжі•пјҡи®Ўз®—жҹҘиҜўзҹ©йҳөQпјҲnГ—dkпјүе’Ңй”®зҹ©йҳөKпјҲnГ—dkпјүзҡ„иҪ¬зҪ®зҡ„д№ҳз§ҜпјҢеҫ—еҲ°дёҖдёӘnГ—nзҡ„жіЁж„ҸеҠӣеҲҶж•°зҹ©йҳөгҖӮе…¶и®Ўз®—еӨҚжқӮеәҰдёәO(nВІВ·dk) гҖӮ
- Softmaxж“ҚдҪңпјҡеҜ№nГ—nзҡ„жіЁж„ҸеҠӣеҲҶж•°зҹ©йҳөзҡ„жҜҸдёҖиЎҢиҝӣиЎҢsoftmaxеҪ’дёҖеҢ–гҖӮе…¶и®Ўз®—еӨҚжқӮеәҰдёәO(nВІ) гҖӮ
- еҠ жқғжұӮе’Ңпјҡе°ҶеҪ’дёҖеҢ–еҗҺзҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҲnГ—nпјүдёҺеҖјзҹ©йҳөVпјҲnГ—dvпјүзӣёд№ҳпјҢеҫ—еҲ°жңҖз»Ҳзҡ„иҫ“еҮәгҖӮе…¶и®Ўз®—еӨҚжқӮеәҰдёәO(nВІВ·dv) гҖӮ
з»јеҗҲжқҘзңӢпјҢиҮӘжіЁж„ҸеҠӣеұӮзҡ„ж—¶й—ҙеӨҚжқӮеәҰдё»иҰҒз”ұO(nВІВ·d
k)е’ҢO(nВІВ·dv)еҶіе®ҡпјҢеҸҜд»Ҙиҝ‘дјјиЎЁзӨәдёә
O(nВІВ·d) гҖӮиҝҷдёӘеӨҚжқӮеәҰиЎЁжҳҺпјҢи®Ўз®—ж—¶й—ҙйҡҸзқҖеәҸеҲ—й•ҝеәҰзҡ„е№іж–№еўһй•ҝгҖӮ
з©әй—ҙеӨҚжқӮеәҰеҲҶжһҗпјҡ
з©әй—ҙеӨҚжқӮеәҰдё»иҰҒз”ұйңҖиҰҒеӯҳеӮЁзҡ„дёӯй—ҙеҸҳйҮҸеҶіе®ҡгҖӮеңЁиҮӘжіЁж„ҸеҠӣжңәеҲ¶дёӯпјҢжңҖеӨ§зҡ„еҶ…еӯҳж¶ҲиҖ—жқҘиҮӘдәҺеӯҳеӮЁnГ—nзҡ„жіЁж„ҸеҠӣеҲҶж•°зҹ©йҳөгҖӮеӣ жӯӨпјҢе…¶з©әй—ҙеӨҚжқӮеәҰдёә O(nВІ) гҖӮеңЁи®ӯз»ғиҝҮзЁӢдёӯпјҢдёәдәҶиҝӣиЎҢеҸҚеҗ‘дј ж’ӯпјҢиҝҳйңҖиҰҒеӯҳеӮЁжҜҸдёҖеұӮзҡ„жҝҖжҙ»еҖјпјҢиҝҷиҝӣдёҖжӯҘеҠ еү§дәҶеҶ…еӯҳзҡ„ж¶ҲиҖ—гҖӮеҜ№дәҺдёҖдёӘжңүNеұӮзҡ„TransformerжЁЎеһӢпјҢе…¶жҖ»жҝҖжҙ»еҶ…еӯҳеҚ з”ЁеҸҜд»ҘиҫҫеҲ°жғҠдәәзҡ„зЁӢеәҰпјҢдҪҝеҫ—еӨ„зҗҶй•ҝеәҸеҲ—еҸҳеҫ—дёҚеҲҮе®һйҷ… гҖӮ
дёӢиЎЁжҖ»з»“дәҶдёҚеҗҢеәҸеҲ—ж“ҚдҪңеұӮзҡ„еӨҚжқӮеәҰеҜ№жҜ”пјҢж•°жҚ®жқҘжәҗдәҺгҖҠAttention Is All You NeedгҖӢи®әж–ҮеҸҠзӣёе…іи§ЈиҜ» пјҡ
| еұӮзұ»еһӢ | и®Ўз®—еӨҚжқӮеәҰ | йЎәеәҸи®Ўз®—йҮҸ | жңҖеӨ§и·Ҝеҫ„й•ҝеәҰ |
|---|
| **иҮӘжіЁж„ҸеҠӣ (Self-Attention)** | **O(nВІВ·d)** | **O(1)** | **O(1)** |
| еҫӘзҺҜзҘһз»ҸзҪ‘з»ң (RNN) | O(nВ·dВІ) | O(n) | O(n) |
| еҚ·з§ҜзҘһз»ҸзҪ‘з»ң (CNN) | O(nВ·kВ·dВІ) | O(1) | O(logвӮ–(n)) |
д»ҺиЎЁдёӯеҸҜд»ҘзңӢеҮәпјҢиҮӘжіЁж„ҸеҠӣеұӮеңЁе№¶иЎҢеҢ–иғҪеҠӣпјҲйЎәеәҸи®Ўз®—йҮҸдёәO(1)пјүе’ҢжҚ•жҚүй•ҝи·қзҰ»дҫқиө–пјҲжңҖеӨ§и·Ҝеҫ„й•ҝеәҰдёәO(1)пјүж–№йқўе…·жңүж— дёҺдјҰжҜ”зҡ„дјҳеҠҝгҖӮ然иҖҢпјҢе…¶O(nВІВ·d)зҡ„и®Ўз®—еӨҚжқӮеәҰеңЁеӨ„зҗҶй•ҝеәҸеҲ—ж—¶пјҢе…¶ејҖй”Җдјҡиҝңи¶…RNNе’ҢCNNпјҢжҲҗдёәе…¶дё»иҰҒзҡ„жҖ§иғҪ瓶йўҲгҖӮ
1.1.3 еҜ№й•ҝеәҸеҲ—еӨ„зҗҶзҡ„йҷҗеҲ¶
дәҢж¬Ўж–№еӨҚжқӮеәҰеҜ№й•ҝеәҸеҲ—еӨ„зҗҶзҡ„йҷҗеҲ¶жҳҜе…Ёж–№дҪҚзҡ„пјҢе®ғдёҚд»…еҪұе“ҚжЁЎеһӢзҡ„и®ӯз»ғж•ҲзҺҮпјҢд№ҹйҷҗеҲ¶дәҶе…¶еңЁе®һйҷ…еә”з”Ёдёӯзҡ„еҸҜиЎҢжҖ§гҖӮйҰ–е…ҲпјҢеңЁи®ӯз»ғйҳ¶ж®өпјҢе·ЁеӨ§зҡ„и®Ўз®—е’ҢеҶ…еӯҳйңҖжұӮж„Ҹе‘ізқҖи®ӯз»ғеӨ§еһӢTransformerжЁЎеһӢйңҖиҰҒеәһеӨ§зҡ„и®Ўз®—йӣҶзҫӨпјҲеҰӮж•°еҚҒз”ҡиҮіж•°зҷҫдёӘй«ҳз«ҜGPUпјүпјҢ并且и®ӯз»ғж—¶й—ҙйқһеёёжј«й•ҝпјҢиҝҷдҪҝеҫ—дёӯе°ҸеһӢз ”з©¶жңәжһ„е’ҢдёӘдәәз ”з©¶иҖ…йҡҫд»ҘеҸӮдёҺеүҚжІҝжЁЎеһӢзҡ„з ”еҸ‘ гҖӮе…¶ж¬ЎпјҢеңЁжҺЁзҗҶйҳ¶ж®өпјҢеҚідҪҝжҳҜе·Із»Ҹи®ӯз»ғеҘҪзҡ„жЁЎеһӢпјҢеӨ„зҗҶй•ҝеәҸеҲ—пјҲдҫӢеҰӮпјҢи¶…иҝҮ2048жҲ–4096дёӘtokenпјүд№ҹеҸҜиғҪеҜјиҮҙеҶ…еӯҳжәўеҮәпјҲOut of Memoryпјү жҲ–е“Қеә”ж—¶й—ҙиҝҮй•ҝпјҢиҝҷйҷҗеҲ¶дәҶе…¶еңЁйңҖиҰҒеӨ„зҗҶй•ҝж–ҮжЎЈгҖҒй•ҝеҜ№иҜқжҲ–й«ҳеҲҶиҫЁзҺҮеӣҫеғҸзӯүеңәжҷҜдёӢзҡ„еә”з”ЁгҖӮдёәдәҶзј“и§ЈиҝҷдёӘй—®йўҳпјҢз ”з©¶дәәе‘ҳжҸҗеҮәдәҶеӨҡз§ҚдјҳеҢ–ж–№жЎҲпјҢдҫӢеҰӮзЁҖз–ҸжіЁж„ҸеҠӣпјҲSparse AttentionпјүгҖҒзәҝжҖ§жіЁж„ҸеҠӣпјҲLinear Attentionпјүе’ҢеҹәдәҺзҠ¶жҖҒз©әй—ҙжЁЎеһӢпјҲSSMпјүзҡ„жһ¶жһ„пјҲеҰӮMambaпјүпјҢиҝҷдәӣж–№жЎҲж—ЁеңЁе°ҶеӨҚжқӮеәҰйҷҚдҪҺеҲ°иҝ‘зәҝжҖ§жҲ–зәҝжҖ§зә§еҲ«пјҢд»ҺиҖҢдҪҝTransformerиғҪеӨҹжӣҙй«ҳж•Ҳең°еӨ„зҗҶй•ҝеәҸеҲ—д»»еҠЎ гҖӮ
1.2 вҖңй»‘зӣ’вҖқй—®йўҳ
дёҺL2е№іж–№еӨҚжқӮеәҰиҝҷдёҖжҳҺзЎ®зҡ„жҖ§иғҪ瓶йўҲдёҚеҗҢпјҢвҖңй»‘зӣ’вҖқй—®йўҳжӣҙеӨҡең°жҢҮеҗ‘дәҶTransformerжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§пјҲInterpretabilityпјү е’ҢйҖҸжҳҺеәҰпјҲTransparencyпјү гҖӮе°Ҫз®ЎиҮӘжіЁж„ҸеҠӣжңәеҲ¶жң¬иә«жҸҗдҫӣдәҶдёҖз§Қи§ӮеҜҹжЁЎеһӢе…іжіЁиҫ“е…ҘеәҸеҲ—е“ӘдәӣйғЁеҲҶзҡ„ж–№ејҸпјҢдҪҶйҡҸзқҖжЁЎеһӢеұӮж•°е’ҢеҸӮж•°йҮҸзҡ„жҖҘеү§еўһеҠ пјҢж•ҙдёӘжЁЎеһӢзҡ„еҶізӯ–иҝҮзЁӢеҸҳеҫ—жһҒе…¶еӨҚжқӮпјҢйҡҫд»Ҙз”Ёз®ҖеҚ•зҡ„规еҲҷжҲ–йҖ»иҫ‘жқҘзҗҶи§Је’Ңи§ЈйҮҠ гҖӮиҝҷз§ҚдёҚеҸҜи§ЈйҮҠжҖ§дёҚд»…йҳ»зўҚдәҶжҲ‘们еҜ№жЁЎеһӢеҶ…йғЁе·ҘдҪңеҺҹзҗҶзҡ„ж·ұе…ҘзҗҶи§ЈпјҢд№ҹеёҰжқҘдәҶе®үе…ЁгҖҒе…¬е№іе’ҢдҝЎд»»зӯүж–№йқўзҡ„йЈҺйҷ©пјҢе°Өе…¶жҳҜеңЁеҢ»з–—гҖҒйҮ‘иһҚгҖҒжі•еҫӢзӯүй«ҳйЈҺйҷ©еҶізӯ–йўҶеҹҹгҖӮ
1.2.1 жЁЎеһӢеҸҜи§ЈйҮҠжҖ§зҡ„зјәеӨұ
TransformerжЁЎеһӢзҡ„вҖңй»‘зӣ’вҖқзү№жҖ§дё»иҰҒдҪ“зҺ°еңЁе…¶еҶізӯ–иҝҮзЁӢзҡ„дёҚеҸҜзҹҘжҖ§гҖӮеҪ“дёҖдёӘжЁЎеһӢеҒҡеҮәйў„жөӢж—¶пјҲдҫӢеҰӮпјҢе°ҶдёҖеҸҘиҜқеҲҶзұ»дёәвҖңжӯЈйқўжғ…з»ӘвҖқпјүпјҢжҲ‘们еҫҲйҡҫзЎ®еҲҮең°зҹҘйҒ“е®ғжҳҜдҫқжҚ®е“Әдәӣиҫ“е…Ҙзү№еҫҒгҖҒйҖҡиҝҮжҖҺж ·зҡ„еҶ…йғЁйҖ»иҫ‘еҫ—еҮәиҝҷдёӘз»“и®әзҡ„гҖӮиҷҪ然еҸҜд»ҘйҖҡиҝҮеҸҜи§ҶеҢ–жіЁж„ҸеҠӣжқғйҮҚжқҘи§ӮеҜҹжЁЎеһӢеңЁзү№е®ҡеұӮе’Ңзү№е®ҡеӨҙдёӯе…іжіЁдәҶе“ӘдәӣиҜҚпјҢдҪҶиҝҷ并дёҚиғҪе®Ңе…Ёи§ЈйҮҠжЁЎеһӢзҡ„еҶізӯ–иҝҮзЁӢгҖӮйҰ–е…ҲпјҢжіЁж„ҸеҠӣжқғйҮҚеҸӘжҳҜжЁЎеһӢеҶ…йғЁзҠ¶жҖҒзҡ„дёҖдёӘдҫ§йқўеҸҚжҳ пјҢе®ғеҸҜиғҪ并дёҚзӣҙжҺҘеҜ№еә”дәҺжңҖз»Ҳзҡ„еҶізӯ–дҫқжҚ®гҖӮе…¶ж¬ЎпјҢдёҖдёӘTransformerжЁЎеһӢйҖҡеёёеҢ…еҗ«ж•°еҚҒеұӮе’ҢдёҠзҷҫдёӘеӨҙпјҢиҝҷдәӣжіЁж„ҸеҠӣжЁЎејҸеҰӮдҪ•зӣёдә’дҪңз”ЁгҖҒеҰӮдҪ•йҖҗеұӮдј йҖ’е’ҢиҪ¬жҚўдҝЎжҒҜпјҢе…¶ж•ҙдҪ“иЎҢдёәжҳҜжһҒе…¶еӨҚжқӮзҡ„пјҢйҡҫд»ҘиҝӣиЎҢе…ЁеұҖжҖ§зҡ„иҝҪиёӘе’ҢзҗҶи§Ј гҖӮиҝҷз§ҚеҸҜи§ЈйҮҠжҖ§зҡ„зјәеӨұпјҢдҪҝеҫ—жЁЎеһӢи°ғиҜ•еҸҳеҫ—еӣ°йҡҫпјҢеҪ“жЁЎеһӢеҮәзҺ°й”ҷиҜҜж—¶пјҢжҲ‘们еҫҲйҡҫе®ҡдҪҚй—®йўҳж №жәҗ并иҝӣиЎҢдҝ®еӨҚгҖӮ
1.2.2 й«ҳз»ҙеј йҮҸж“ҚдҪңзҡ„дёҚеҸҜиҝҪиёӘжҖ§
и®әж–ҮгҖҠAttention Is Not What You NeedгҖӢж·ұеҲ»ең°жҢҮеҮәдәҶTransformerвҖңй»‘зӣ’вҖқй—®йўҳзҡ„ж №жәҗпјҢеҚіе…¶ж ёеҝғж“ҚдҪңжҳҜдёҖз§Қ вҖңй«ҳз»ҙеј йҮҸжҸҗеҚҮвҖқпјҲtensor liftingпјү гҖӮе…·дҪ“жқҘиҜҙпјҢиҮӘжіЁж„ҸеҠӣжңәеҲ¶е°ҶжҜҸдёӘtokenзҡ„dз»ҙйҡҗи—ҸзҠ¶жҖҒеҗ‘йҮҸhtпјҢйҖҡиҝҮдёҺе…¶д»–жүҖжңүдҪҚзҪ®зҡ„tokenиҝӣиЎҢдәӨдә’пјҢжҸҗеҚҮеҲ°дёҖдёӘLГ—Lзҡ„жҲҗеҜ№е…је®№жҖ§еј йҮҸз©әй—ҙгҖӮиҝҷдёӘеј йҮҸз©әй—ҙзҡ„з»ҙеәҰжһҒй«ҳпјҢеҢ…еҗ«дәҶLВІдёӘе…ғзҙ пјҲеҜ№дәҺжҜҸдёӘжіЁж„ҸеҠӣеӨҙпјүгҖӮжЁЎеһӢеңЁиҝҷдёӘе·ЁеӨ§зҡ„еј йҮҸз©әй—ҙдёӯиҝӣиЎҢж“ҚдҪңпјҢ然еҗҺеҶҚжҠ•еҪұеӣһеҺҹе§Ӣзҡ„йҡҗи—ҸзҠ¶жҖҒз©әй—ҙгҖӮиҝҷз§Қж“ҚдҪңзҡ„вҖңиҮӘз”ұеәҰвҖқпјҲdegrees of freedomпјүйқһеёёеӨ§пјҢе°Өе…¶жҳҜеңЁеӨҡеұӮе’ҢеӨҡеӨҙзҡ„TransformerдёӯпјҢжЁЎеһӢеҶ…йғЁзҡ„жңүж•ҲзҠ¶жҖҒж¶үеҸҠеҲ°дёҖдёӘдёҚж–ӯжј”еҢ–зҡ„жіЁж„ҸеҠӣеј йҮҸдә‘гҖӮд»ҺеҮ дҪ•и§’еәҰзңӢпјҢиҝҷзӣёеҪ“дәҺе°ҶеәҸеҲ—д»ҺtokenиЎЁзӨәзҡ„жөҒеҪўжҸҗеҚҮеҲ°дёҖдёӘжӣҙеӨ§зҡ„жҲҗеҜ№дәӨдә’з©әй—ҙгҖӮиҝҷз§ҚжҸҗеҚҮиҷҪ然иөӢдәҲдәҶжЁЎеһӢејәеӨ§зҡ„иЎЁиҫҫиғҪеҠӣпјҢдҪҶд№ҹдҪҝе…¶иЎҢдёәеңЁж•°еӯҰдёҠеҸҳеҫ— вҖңдёҚеҸҜиҝҪиёӘвҖқпјҲnon-traceableпјү гҖӮжҲ‘们зјәд№ҸдёҖдёӘе°Ҹзҡ„гҖҒжҳҺзЎ®зҡ„ж•°еӯҰдёҚеҸҳйҮҸж—ҸжқҘжҸҸиҝ°жЁЎеһӢеңЁжүҖжңүеұӮе’ҢеӨҙдёҠзҡ„е…ЁеұҖж•Ҳеә”пјҢиҝҷдҪҝеҫ—еҜ№жЁЎеһӢиҝӣиЎҢдёҘи°Ёзҡ„еҲҶжһҗе’Ңи§ЈйҮҠеҸҳеҫ—ејӮеёёеӣ°йҡҫгҖӮ
1.2.3 еҜ№жЁЎеһӢдҝЎд»»еәҰе’Ңеә”з”Ёзҡ„еҪұе“Қ
вҖңй»‘зӣ’вҖқй—®йўҳеҜ№жЁЎеһӢзҡ„е®һйҷ…еә”з”Ёе’ҢйғЁзҪІжһ„жҲҗдәҶдёҘйҮҚжҢ‘жҲҳгҖӮеңЁйңҖиҰҒй«ҳеҸҜйқ жҖ§е’Ңе®үе…ЁжҖ§зҡ„йўҶеҹҹпјҢеҰӮжһңдёҖдёӘжЁЎеһӢзҡ„еҶізӯ–иҝҮзЁӢж— жі•иў«зҗҶи§Је’ҢйӘҢиҜҒпјҢйӮЈд№Ҳз”ЁжҲ·е’Ңзӣ‘з®Ўжңәжһ„е°ұеҫҲйҡҫдҝЎд»»е®ғгҖӮдҫӢеҰӮпјҢеңЁиҮӘеҠЁй©ҫ驶系з»ҹдёӯпјҢеҰӮжһңдёҖдёӘTransformerжЁЎеһӢиҙҹиҙЈиҜҶеҲ«дәӨйҖҡж Үеҝ—пјҢдҪҶе·ҘзЁӢеёҲж— жі•и§ЈйҮҠе®ғдёәдҪ•дјҡе°ҶдёҖдёӘвҖңеҒңжӯўвҖқж Үеҝ—иҜҜеҲӨдёәвҖңйҷҗйҖҹвҖқж Үеҝ—пјҢйӮЈд№ҲиҝҷдёӘзі»з»ҹе°ұж— жі•иў«е®үе…Ёең°йғЁзҪІгҖӮжӯӨеӨ–пјҢдёҚеҸҜи§ЈйҮҠжҖ§д№ҹдҪҝеҫ—жЁЎеһӢе®№жҳ“еҸ—еҲ°еҜ№жҠ—жҖ§ж”»еҮ»пјҲAdversarial Attacksпјү зҡ„еҪұе“ҚгҖӮж”»еҮ»иҖ…еҸҜд»ҘеҲ©з”ЁжЁЎеһӢзҡ„дёҚеҸҜзҹҘжҖ§пјҢжһ„йҖ еҮәзңӢдјјжӯЈеёёдҪҶиғҪеӨҹж¬әйӘ—жЁЎеһӢзҡ„иҫ“е…ҘпјҢд»ҺиҖҢеј•еҸ‘й”ҷиҜҜзҡ„иҫ“еҮә гҖӮдёәдәҶи§ЈеҶівҖңй»‘зӣ’вҖқй—®йўҳпјҢз ”з©¶дәәе‘ҳжӯЈеңЁз§ҜжһҒжҺўзҙўеҗ„з§ҚеҸҜи§ЈйҮҠжҖ§AIпјҲXAIпјүжҠҖжңҜпјҢеҢ…жӢ¬жЁЎеһӢж— е…ізҡ„ж–№жі•пјҲеҰӮLIMEе’ҢSHAPпјүе’ҢжЁЎеһӢзү№е®ҡзҡ„ж–№жі•пјҲеҰӮжіЁж„ҸеҠӣжңәеҲ¶еҲҶжһҗпјүпјҢж—ЁеңЁжү“ејҖжЁЎеһӢзҡ„вҖңй»‘зӣ’вҖқпјҢжҸҗй«ҳе…¶еҶізӯ–зҡ„йҖҸжҳҺеәҰе’ҢеҸҜдҝЎеәҰ гҖӮеҗҢж—¶пјҢд№ҹжңүз ”з©¶е°қиҜ•д»Һж №жң¬дёҠйҮҚж–°и®ҫи®ЎжЁЎеһӢжһ¶жһ„пјҢдҫӢеҰӮжҸҗеҮәвҖңзҷҪзӣ’вҖқTransformerпјҢдҪҝе…¶еңЁи®ҫи®ЎдёҠе°ұе…·еӨҮжӣҙеҘҪзҡ„еҸҜи§ЈйҮҠжҖ§ гҖӮ
2. зҺ°жңүжӣҝд»Јж–№жЎҲз»јиҝ°
дёәдәҶеә”еҜ№TransformerжЁЎеһӢйқўдёҙзҡ„L2е№іж–№еӨҚжқӮеәҰе’ҢвҖңй»‘зӣ’вҖқдёӨеӨ§ж ёеҝғжҢ‘жҲҳпјҢеӯҰжңҜз•Ңе’Ңе·Ҙдёҡз•Ңж¶ҢзҺ°еҮәеӨ§йҮҸеҲӣж–°жҖ§зҡ„жӣҝд»Јж–№жЎҲе’ҢдјҳеҢ–ж–№жі•гҖӮиҝҷдәӣж–№жЎҲд»ҺдёҚеҗҢи§’еәҰеҲҮе…ҘпјҢжңүзҡ„иҮҙеҠӣдәҺеңЁдҝқжҢҒжҖ§иғҪзҡ„еҗҢж—¶йҷҚдҪҺи®Ўз®—еӨҚжқӮеәҰпјҢжңүзҡ„еҲҷдё“жіЁдәҺжҸҗеҚҮжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§гҖӮиҝҷдәӣз ”з©¶дёҚд»…жҺЁеҠЁдәҶTransformerжһ¶жһ„зҡ„жј”иҝӣпјҢд№ҹдёәи§ЈеҶіжӣҙеӨҚжқӮзҡ„AIй—®йўҳжҸҗдҫӣдәҶж–°зҡ„жҖқи·ҜгҖӮ
2.1 й’ҲеҜ№L2е№іж–№еӨҚжқӮеәҰзҡ„дјҳеҢ–ж–№жЎҲ
й’ҲеҜ№иҮӘжіЁж„ҸеҠӣжңәеҲ¶зҡ„дәҢж¬Ўж–№еӨҚжқӮеәҰй—®йўҳпјҢз ”з©¶дәәе‘ҳжҸҗеҮәдәҶеӨҡз§ҚдјҳеҢ–зӯ–з•ҘпјҢе…¶ж ёеҝғжҖқжғіжҳҜеҮҸе°‘йңҖиҰҒи®Ўз®—зҡ„tokenеҜ№ж•°йҮҸпјҢжҲ–иҖ…йҖҡиҝҮж•°еӯҰиҝ‘дјјжқҘйҷҚдҪҺи®Ўз®—еӨҚжқӮеәҰгҖӮиҝҷдәӣж–№жі•еӨ§иҮҙеҸҜд»ҘеҲҶдёәзЁҖз–ҸжіЁж„ҸеҠӣгҖҒзәҝжҖ§жіЁж„ҸеҠӣгҖҒдҪҺ秩иҝ‘дјје’ҢеҲҶеқ—ж–№жі•зӯүеҮ еӨ§зұ»гҖӮ
2.1.1 зЁҖз–ҸжіЁж„ҸеҠӣпјҲSparse Attentionпјү
зЁҖз–ҸжіЁж„ҸеҠӣпјҲSparse Attentionпјүзҡ„ж ёеҝғжҖқжғіжҳҜпјҢ并йқһжүҖжңүtokenеҜ№д№Ӣй—ҙзҡ„дәӨдә’йғҪжҳҜеҗҢзӯүйҮҚиҰҒзҡ„гҖӮеӣ жӯӨпјҢеҸҜд»ҘйҖҡиҝҮйҷҗеҲ¶жҜҸдёӘtokenеҸӘиғҪе…іжіЁеҲ°еәҸеҲ—дёӯзҡ„дёҖе°ҸйғЁеҲҶе…¶д»–tokenпјҢжқҘжҳҫи‘—йҷҚдҪҺи®Ўз®—зҡ„еӨҚжқӮеәҰгҖӮиҝҷз§Қж–№жі•е°ҶеҺҹжң¬зЁ еҜҶзҡ„nГ—nжіЁж„ҸеҠӣзҹ©йҳөжӣҝжҚўдёәдёҖдёӘзЁҖз–Ҹзҹ©йҳөпјҢд»ҺиҖҢе°Ҷи®Ўз®—еӨҚжқӮеәҰйҷҚдҪҺеҲ°иҝ‘зәҝжҖ§ж°ҙе№іпјҢдҫӢеҰӮO(nВ·log n)жҲ–O(n) гҖӮ
е…·дҪ“зҡ„зЁҖз–ҸжЁЎејҸи®ҫи®ЎеӨҡз§ҚеӨҡж ·пјҢе…¶дёӯдёҖдәӣд»ЈиЎЁжҖ§зҡ„е·ҘдҪңеҢ…жӢ¬пјҡ
LongformerпјҡйҮҮз”Ёж»‘еҠЁзӘ—еҸЈжіЁж„ҸеҠӣпјҲSliding Window Attentionпјү пјҢеҚіжҜҸдёӘtokenеҸӘе…іжіЁе…¶йӮ»иҝ‘зҡ„wдёӘtokenгҖӮжӯӨеӨ–пјҢе®ғиҝҳеј•е…ҘдәҶе…ЁеұҖжіЁж„ҸеҠӣпјҲGlobal Attentionпјү пјҢе…Ғи®ёе°‘ж•°еҮ дёӘиў«йҖүдёӯзҡ„tokenпјҲеҰӮ[CLS]жҲ–еҸҘйҰ–иҜҚпјүеҸҜд»Ҙе…іжіЁеҲ°еәҸеҲ—дёӯзҡ„жүҖжңүе…¶д»–tokenпјҢд»ҺиҖҢдҝқз•ҷдёҖе®ҡзҡ„е…ЁеұҖдҝЎжҒҜж•ҙеҗҲиғҪеҠӣгҖӮ
BigBirdпјҡз»“еҗҲдәҶдёүз§ҚзЁҖз–ҸжіЁж„ҸеҠӣжЁЎејҸпјҡеұҖйғЁжіЁж„ҸеҠӣпјҲLocal Attentionпјү гҖҒе…ЁеұҖжіЁж„ҸеҠӣпјҲGlobal Attentionпјү е’ҢйҡҸжңәжіЁж„ҸеҠӣпјҲRandom Attentionпјү гҖӮйҡҸжңәжіЁж„ҸеҠӣе…Ғи®ёжҜҸдёӘtokenйҡҸжңәе…іжіЁеәҸеҲ—дёӯзҡ„е…¶д»–rдёӘtokenпјҢиҝҷжңүеҠ©дәҺеңЁзЁҖз–ҸиҝһжҺҘдёӯе»әз«Ӣй•ҝи·қзҰ»дҫқиө–гҖӮ
ReformerпјҡдҪҝз”ЁеұҖйғЁж•Ҹж„ҹе“ҲеёҢпјҲLocality-Sensitive Hashing, LSHпјү жқҘиҜҶеҲ«зӣёдјјзҡ„tokenпјҢ并еҸӘеңЁиҝҷдәӣзӣёдјјзҡ„tokenд№Ӣй—ҙи®Ўз®—жіЁж„ҸеҠӣгҖӮиҝҷз§Қж–№жі•е°ҶеӨҚжқӮеәҰд»ҺO(LВІ)йҷҚдҪҺеҲ°O(LВ·log L) пјҢе…¶дёӯLжҳҜеәҸеҲ—й•ҝеәҰ гҖӮ
зЁҖз–ҸжіЁж„ҸеҠӣж–№жі•йҖҡиҝҮзүәзүІйғЁеҲҶе…ЁеұҖдәӨдә’иғҪеҠӣжқҘжҚўеҸ–и®Ўз®—ж•ҲзҺҮпјҢеңЁи®ёеӨҡй•ҝеәҸеҲ—д»»еҠЎдёҠеҸ–еҫ—дәҶдёҺе…ЁжіЁж„ҸеҠӣжЁЎеһӢзӣёеҪ“з”ҡиҮіжӣҙеҘҪзҡ„жҖ§иғҪпјҢеӣ дёәе®ғеҸҜиғҪжңүеҠ©дәҺжЁЎеһӢе…іжіЁеұҖйғЁз»“жһ„пјҢ并еҮҸе°‘еҷӘеЈ°е№Іжү°гҖӮ
2.1.2 зәҝжҖ§жіЁж„ҸеҠӣпјҲLinear Attentionпјү
зәҝжҖ§жіЁж„ҸеҠӣпјҲLinear AttentionпјүжҳҜеҸҰдёҖзұ»йҮҚиҰҒзҡ„дјҳеҢ–ж–№жі•пјҢе®ғйҖҡиҝҮдҪҝз”Ёж ёеҮҪж•°пјҲKernel FunctionпјүжқҘиҝ‘дјјsoftmaxжіЁж„ҸеҠӣжңәеҲ¶пјҢд»ҺиҖҢе°Ҷи®Ўз®—еӨҚжқӮеәҰйҷҚдҪҺеҲ°дёҘж јзҡ„зәҝжҖ§зә§еҲ«O(n) гҖӮе…¶ж ёеҝғжҖқжғіжҳҜеҲ©з”Ёзҹ©йҳөд№ҳжі•зҡ„з»“еҗҲеҫӢпјҢж”№еҸҳи®Ўз®—зҡ„йЎәеәҸпјҢйҒҝе…ҚжҳҫејҸең°и®Ўз®—е’ҢеӯҳеӮЁnГ—nзҡ„жіЁж„ҸеҠӣзҹ©йҳө гҖӮ
ж ҮеҮҶзҡ„иҮӘжіЁж„ҸеҠӣи®Ўз®—еҸҜд»ҘиЎЁзӨәдёә softmax(QKбөҖ)VгҖӮзәҝжҖ§жіЁж„ҸеҠӣж–№жі•йҖҡиҝҮеј•е…Ҙж ёеҮҪж•° ПҶ(В·)пјҢе°Ҷе…¶иҝ‘дјјдёә ПҶ(Q)(ПҶ(K)бөҖV)гҖӮйҖҡиҝҮиҝҷз§Қж–№ејҸпјҢеҸҜд»Ҙе…Ҳи®Ўз®— ПҶ(K)бөҖVпјҢе…¶еӨҚжқӮеәҰдёәO(nВ·dВІ)пјҢ然еҗҺеҶҚдёҺ ПҶ(Q) зӣёд№ҳпјҢеҫ—еҲ°жңҖз»Ҳз»“жһңгҖӮж•ҙдёӘиҝҮзЁӢзҡ„еӨҚжқӮеәҰдёҺеәҸеҲ—й•ҝеәҰnжҲҗзәҝжҖ§е…ізі»гҖӮ
дёҖдәӣд»ЈиЎЁжҖ§зҡ„зәҝжҖ§жіЁж„ҸеҠӣжЁЎеһӢеҢ…жӢ¬пјҡ
LinformerпјҡйҖҡиҝҮдҪҺ秩жҠ•еҪұжқҘиҝ‘дјјsoftmaxжіЁж„ҸеҠӣзҹ©йҳөпјҢиҜҒжҳҺдәҶиҮӘжіЁж„ҸеҠӣзҹ©йҳөйҖҡеёёжҳҜдҪҺ秩зҡ„пјҢд»ҺиҖҢеҸҜд»Ҙз”ЁзәҝжҖ§еӨҚжқӮеәҰжқҘиҝ‘дјји®Ўз®— гҖӮ
PerformerпјҡдҪҝз”ЁдёҖз§Қж–°йў–зҡ„еҝ«йҖҹжіЁж„ҸеҠӣйҖҡиҝҮжӯЈдәӨйҡҸжңәзү№еҫҒпјҲFAVOR+пјү ж–№жі•жқҘиҝ‘дјјsoftmaxжіЁж„ҸеҠӣж ёпјҢиғҪеӨҹд»ҘеҸҜиҜҒжҳҺзҡ„еҮҶзЎ®жҖ§дј°и®Ўеёёи§„зҡ„全秩注ж„ҸеҠӣTransformerпјҢдҪҶд»…дҪҝз”ЁзәҝжҖ§з©әй—ҙе’Ңж—¶й—ҙеӨҚжқӮеәҰ гҖӮ
FlashAttentionпјҡиҷҪ然дёҘж јжқҘиҜҙжҳҜдёҖз§ҚIOж„ҹзҹҘзҡ„зІҫзЎ®и®Ўз®—дјҳеҢ–иҖҢйқһиҝ‘дјјж–№жі•пјҢдҪҶе®ғйҖҡиҝҮе·§еҰҷең°еҲ©з”ЁGPUзҡ„еҶ…еӯҳеұӮж¬Ўз»“жһ„пјҲHBMе’ҢSRAMпјүпјҢйҒҝе…ҚдәҶе®һдҫӢеҢ–е·ЁеӨ§зҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҢд»ҺиҖҢжһҒеӨ§ең°еҠ йҖҹдәҶж ҮеҮҶжіЁж„ҸеҠӣзҡ„计算并йҷҚдҪҺдәҶеҶ…еӯҳеҚ з”ЁпјҢе…¶ж•ҲжһңдёҺзәҝжҖ§жіЁж„ҸеҠӣзұ»дјјпјҢж·ұеҲ»еҪұе“ҚдәҶеҗҺз»ӯзҡ„жһ¶жһ„и®ҫи®Ў гҖӮ
зәҝжҖ§жіЁж„ҸеҠӣж–№жі•еңЁзҗҶи®әдёҠе…·жңүжңҖдјҳзҡ„еӨҚжқӮеәҰпјҢдҪҶеңЁе®һи·өдёӯпјҢе…¶жҖ§иғҪжңүж—¶дјҡз•ҘдҪҺдәҺж ҮеҮҶзҡ„softmaxжіЁж„ҸеҠӣпјҢе°Өе…¶жҳҜеңЁзҹӯеәҸеҲ—д»»еҠЎдёҠгҖӮжӯӨеӨ–пјҢдёҖдәӣзәҝжҖ§жіЁж„ҸеҠӣж–№жі•пјҲеҰӮPerformerпјүдёҺзӣёеҜ№дҪҚзҪ®зј–з ҒзӯүжңәеҲ¶дёҚе…је®№пјҢйҷҗеҲ¶дәҶе…¶еә”з”ЁиҢғеӣҙ гҖӮ
2.1.3 дҪҺ秩иҝ‘дјјдёҺеҲҶеқ—ж–№жі•
йҷӨдәҶзЁҖз–ҸжіЁж„ҸеҠӣе’ҢзәҝжҖ§жіЁж„ҸеҠӣпјҢиҝҳжңүдёҖдәӣе…¶д»–жңүж•Ҳзҡ„дјҳеҢ–ж–№жі•гҖӮ
дҪҺ秩иҝ‘дјјпјҲLow-Rank Approximationпјү пјҡиҜҘж–№жі•еҹәдәҺи§ӮеҜҹеҸ‘зҺ°пјҢиҮӘжіЁж„ҸеҠӣзҹ©йҳөйҖҡеёёжҳҜдҪҺ秩зҡ„гҖӮеӣ жӯӨпјҢеҸҜд»ҘйҖҡиҝҮеҘҮејӮеҖјеҲҶи§ЈпјҲSVDпјүзӯүж–№жі•пјҢз”ЁдёӨдёӘдҪҺ秩зҹ©йҳөзҡ„д№ҳз§ҜжқҘиҝ‘дјјеҺҹе§Ӣзҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҢд»ҺиҖҢйҷҚдҪҺи®Ўз®—е’ҢеӯҳеӮЁејҖй”ҖгҖӮ
еҲҶеқ—ж–№жі•пјҲBlockwise Attentionпјү пјҡиҜҘж–№жі•е°Ҷиҫ“е…ҘеәҸеҲ—еҲ’еҲҶдёәиӢҘе№ІдёӘеӣәе®ҡеӨ§е°Ҹзҡ„еқ—пјҢ然еҗҺеңЁжҜҸдёӘеқ—еҶ…йғЁиҝӣиЎҢе…ЁжіЁж„ҸеҠӣи®Ўз®—пјҢжҲ–иҖ…еңЁдёҚеҗҢеқ—д№Ӣй—ҙиҝӣиЎҢзЁҖз–Ҹзҡ„жіЁж„ҸеҠӣдәӨдә’гҖӮиҝҷз§Қж–№жі•еҸҜд»Ҙжңүж•Ҳең°е°Ҷ计算并иЎҢеҢ–пјҢ并йҷҚдҪҺеҶ…еӯҳеҚ з”ЁгҖӮ
зҠ¶жҖҒз©әй—ҙжЁЎеһӢпјҲState Space Models, SSMпјү пјҡиҝҷжҳҜдёҖзұ»еҪ»еә•ж‘Ҷи„ұжіЁж„ҸеҠӣжңәеҲ¶зҡ„жӣҝд»Јжһ¶жһ„пјҢеҰӮMambaжЁЎеһӢгҖӮSSMйҖҡиҝҮзҠ¶жҖҒз©әй—ҙж–№зЁӢе’Ң硬件ж„ҹзҹҘзҡ„并иЎҢжү«жҸҸз®—жі•пјҢе®һзҺ°дәҶзәҝжҖ§еӨҚжқӮеәҰзҡ„й•ҝеәҸеҲ—е»әжЁЎпјҢеңЁй•ҝдёҠдёӢж–Үд»»еҠЎдёҠеұ•зҺ°еҮәеҚ“и¶Ҡзҡ„жҖ§иғҪе’Ңж•ҲзҺҮ гҖӮ
иҝҷдәӣдјҳеҢ–ж–№жЎҲжһҒеӨ§ең°жү©еұ•дәҶTransformerзҡ„еә”з”Ёиҫ№з•ҢпјҢдҪҝе…¶иғҪеӨҹеӨ„зҗҶи¶ҠжқҘи¶Ҡй•ҝзҡ„еәҸеҲ—пјҢ并жҺЁеҠЁдәҶеӨ§еһӢиҜӯиЁҖжЁЎеһӢпјҲLLMпјүзҡ„еҝ«йҖҹеҸ‘еұ•гҖӮ
2.2 й’ҲеҜ№вҖңй»‘зӣ’вҖқй—®йўҳзҡ„и§ЈеҶіж–№жЎҲ
дёҺL2еӨҚжқӮеәҰй—®йўҳзӣёжҜ”пјҢвҖңй»‘зӣ’вҖқй—®йўҳзҡ„и§ЈеҶіж–№жЎҲжӣҙеҠ еӨҡж ·еҢ–пјҢеӣ дёәе®ғдёҚд»…ж¶үеҸҠжҠҖжңҜеұӮйқўпјҢиҝҳж¶үеҸҠеҜ№жЁЎеһӢеҸҜи§ЈйҮҠжҖ§зҡ„е“ІеӯҰжҖқиҖғгҖӮзӣ®еүҚпјҢдё»иҰҒзҡ„и§ЈеҶіжҖқи·ҜеҸҜд»ҘеҲҶдёәдёӨеӨ§зұ»пјҡдәӢеҗҺи§ЈйҮҠпјҲPost-hoc Explanationпјүе’ҢжЁЎеһӢеҶ…зҪ®еҸҜи§ЈйҮҠжҖ§пјҲIntrinsic InterpretabilityпјүгҖӮ
2.2.1 зҷҪзӣ’еҢ–Transformerжһ¶жһ„пјҲеҰӮCRATEпјү
дәӢеҗҺи§ЈйҮҠж–№жі•пјҢеҰӮLIMEе’ҢSHAPпјҢиҜ•еӣҫеңЁжЁЎеһӢи®ӯз»ғе®ҢжҲҗеҗҺпјҢйҖҡиҝҮеӨ–йғЁе·Ҙе…·жқҘи§ЈйҮҠе…¶йў„жөӢз»“жһң гҖӮ然иҖҢпјҢиҝҷдәӣж–№жі•жҸҗдҫӣзҡ„и§ЈйҮҠеҸҜиғҪ并дёҚе®Ңе…ЁеҮҶзЎ®жҲ–еҝ е®һдәҺжЁЎеһӢзҡ„зңҹе®һиЎҢдёәгҖӮеӣ жӯӨпјҢи¶ҠжқҘи¶ҠеӨҡзҡ„з ”з©¶ејҖе§Ӣе…іжіЁеҰӮдҪ•д»Һж №жң¬дёҠи®ҫи®ЎеҮәжң¬иә«е°ұе…·еӨҮеҸҜи§ЈйҮҠжҖ§зҡ„вҖңзҷҪзӣ’вҖқжЁЎеһӢгҖӮ
дёҖдёӘд»ЈиЎЁжҖ§зҡ„е·ҘдҪңжҳҜ马жҜ…ж•ҷжҺҲеӣўйҳҹжҸҗеҮәзҡ„CRATEпјҲCoding and Rate Reduction Transformerпјү гҖӮCRATEзҡ„ж ёеҝғжҖқжғіжҳҜд»ҺвҖң第дёҖжҖ§еҺҹзҗҶвҖқеҮәеҸ‘пјҢе°Ҷж·ұеәҰеӯҰд№ зҡ„жң¬иҙЁи§ҶдёәдёҖз§Қж•°жҚ®еҺӢзј©иҝҮзЁӢгҖӮе®ғйҖҡиҝҮе°Ҷй«ҳз»ҙеәҰзҡ„иҫ“е…Ҙж•°жҚ®еҲҶеёғеҺӢзј©еҲ°дҪҺз»ҙзҡ„з»“жһ„еҢ–еҲҶеёғпјҢжқҘеӯҰд№ жңүж•Ҳзҡ„иЎЁеҫҒгҖӮCRATEзҡ„жҜҸдёҖеұӮйғҪжңүжҳҺзЎ®зҡ„ж•°еӯҰзӣ®ж ҮпјҢеҚіжңҖеӨ§еҢ–зј–з ҒзҺҮйҷҚдҪҺпјҲRate Reductionпјү пјҢиҝҷдҪҝеҫ—жЁЎеһӢзҡ„еӯҰд№ иҝҮзЁӢжӣҙеҠ йҖҸжҳҺе’ҢеҸҜи§ЈйҮҠгҖӮCRATEеңЁдҝқжҢҒTransformerз»“жһ„е’ҢеҠҹиғҪдјҳеҠҝзҡ„еҗҢж—¶пјҢеӨ§еӨ§еўһејәдәҶжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§пјҢдёәжү“ејҖLLMзҡ„вҖңй»‘зӣ’вҖқжҸҗдҫӣдәҶдёҖдёӘе…Ёж–°зҡ„жҠҖжңҜи·Ҝеҫ„ гҖӮ
2.2.2 еҹәдәҺеҮ дҪ•жҲ–зү©зҗҶеҺҹзҗҶзҡ„жЁЎеһӢи®ҫи®Ў
еҸҰдёҖзұ»жҸҗеҚҮеҸҜи§ЈйҮҠжҖ§зҡ„ж–№жі•жҳҜе°Ҷж·ұеәҰеӯҰд№ жЁЎеһӢе»әз«ӢеңЁжӣҙеқҡе®һзҡ„ж•°еӯҰжҲ–зү©зҗҶеҹәзЎҖд№ӢдёҠгҖӮйҖҡиҝҮе°ҶжЁЎеһӢзҡ„иҝҗз®—дёҺе…·жңүжҳҺзЎ®еҮ дҪ•жҲ–зү©зҗҶж„Ҹд№үзҡ„ж“ҚдҪңиҒ”зі»иө·жқҘпјҢеҸҜд»ҘдҪҝжЁЎеһӢзҡ„иЎҢдёәжӣҙе®№жҳ“иў«зҗҶи§Је’ҢеҲҶжһҗгҖӮ
дҫӢеҰӮпјҢдёҖдәӣз ”з©¶е°қиҜ•е°ҶзҘһз»ҸзҪ‘з»ңдёҺеҫ®еҲҶж–№зЁӢгҖҒжӢ“жү‘еӯҰжҲ–дҝЎжҒҜеҮ дҪ•зӯүзҗҶи®әзӣёз»“еҗҲгҖӮиҝҷз§Қж–№жі•дёҚд»…жңүеҠ©дәҺжҸҗеҚҮжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§пјҢиҝҳеҸҜиғҪеёҰжқҘжҖ§иғҪдёҠзҡ„жҸҗеҚҮе’ҢжӣҙеҘҪзҡ„жіӣеҢ–иғҪеҠӣгҖӮйҖҡиҝҮе°ҶжЁЎеһӢзҡ„ж ёеҝғж“ҚдҪңд»Һйҡҫд»ҘиҝҪиёӘзҡ„й«ҳз»ҙеј йҮҸж“ҚдҪңпјҢиҪ¬еҸҳдёәеңЁе…·жңүжҳҺзЎ®ж•°еӯҰз»“жһ„зҡ„жөҒеҪўдёҠзҡ„жј”еҢ–иҝҮзЁӢпјҢеҸҜд»ҘдёәжЁЎеһӢзҡ„еҲҶжһҗжҸҗдҫӣејәеӨ§зҡ„зҗҶи®әе·Ҙе…·гҖӮиҝҷз§Қи®ҫи®ЎзҗҶеҝөзҡ„иҪ¬еҸҳпјҢеҸҜиғҪжҳҜжңӘжқҘи§ЈеҶівҖңй»‘зӣ’вҖқй—®йўҳзҡ„е…ій”®ж–№еҗ‘д№ӢдёҖпјҢиҖҢжң¬ж–Үе°ҶиҰҒеҲҶжһҗзҡ„Causal Grassmann TransformerжӯЈжҳҜиҝҷдёҖжҖқи·Ҝзҡ„жқ°еҮәд»ЈиЎЁгҖӮ
3. ж–°жЁЎеһӢеҲҶжһҗпјҡCausal Grassmann Transformer
дёәдәҶеә”еҜ№ж ҮеҮҶTransformerжЁЎеһӢжүҖйқўдёҙзҡ„L2е№іж–№еӨҚжқӮеәҰе’ҢвҖңй»‘зӣ’вҖқй—®йўҳпјҢи®әж–ҮгҖҠAttention Is Not What You NeedгҖӢжҸҗеҮәдәҶдёҖз§ҚеҲӣж–°зҡ„гҖҒе®Ңе…ЁдёҚдҫқиө–жҳҫејҸжіЁж„ҸеҠӣжңәеҲ¶зҡ„еәҸеҲ—жЁЎеһӢвҖ”вҖ”Causal Grassmann TransformerгҖӮиҜҘжЁЎеһӢзҡ„ж ёеҝғжҖқжғіжҳҜпјҢжҲ‘们зңҹжӯЈйңҖиҰҒзҡ„并йқһжіЁж„ҸеҠӣжңәеҲ¶жң¬иә«пјҢиҖҢжҳҜдёҖз§ҚиғҪеӨҹдёәйҡҗи—ҸиЎЁзӨәжҸҗдҫӣи¶іеӨҹиЎЁиҫҫиғҪеҠӣзҡ„ вҖңеҮ дҪ•жј”еҢ–жңәеҲ¶вҖқпјҲgeometric evolution mechanismпјү гҖӮйҖҡиҝҮе°ҶеәҸеҲ—е»әжЁЎй—®йўҳд»Һи®Ўз®—жҲҗеҜ№жіЁж„ҸеҠӣжқғйҮҚиҪ¬жҚўдёәеңЁGrassmannжөҒеҪўдёҠж“ҚдҪңдҪҺз»ҙеӯҗз©әй—ҙзҡ„еҮ дҪ•й—®йўҳпјҢCausal Grassmann TransformerеңЁйҷҚдҪҺи®Ўз®—еӨҚжқӮеәҰзҡ„еҗҢж—¶пјҢд№ҹдёәжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§жҸҗдҫӣдәҶж–°зҡ„йҖ”еҫ„гҖӮиҝҷдёҖи®ҫи®Ўе“ІеӯҰдёҠзҡ„иҪ¬еҸҳпјҢдёәи§ЈеҶіTransformerзҡ„еӣәжңүзјәйҷ·жҸҗдҫӣдәҶдёҖдёӘжһҒе…·жҪңеҠӣзҡ„з»јеҗҲи§ЈеҶіж–№жЎҲгҖӮ
3.1 и®әж–ҮгҖҠAttention Is Not What You NeedгҖӢж ёеҝғжҖқжғі
иҜҘи®әж–Үзҡ„ж ёеҝғи®әзӮ№жҳҜеҜ№вҖңжіЁж„ҸеҠӣжңәеҲ¶жҳҜеәҸеҲ—е»әжЁЎдёҚеҸҜжҲ–зјәзҡ„ж ёеҝғвҖқиҝҷдёҖжҷ®йҒҚи§ӮзӮ№жҸҗеҮәдәҶжҢ‘жҲҳгҖӮдҪңиҖ…и®ӨдёәпјҢжіЁж„ҸеҠӣжңәеҲ¶еҸӘжҳҜе®һзҺ°йҡҗи—ҸиЎЁзӨәеҮ дҪ•жҸҗеҚҮпјҲgeometric liftingпјүзҡ„дёҖз§Қж–№ејҸпјҢиҖҢйқһе”ҜдёҖж–№ејҸгҖӮйҖҡиҝҮе°ҶжЁЎеһӢзҡ„ж ёеҝғж“ҚдҪңд»Һйҡҫд»ҘиҝҪиёӘзҡ„й«ҳз»ҙеј йҮҸз©әй—ҙиҪ¬з§»еҲ°дёҖдёӘж•°еӯҰдёҠжӣҙжҳ“дәҺеҲҶжһҗзҡ„жңүйҷҗз»ҙжөҒеҪўвҖ”вҖ”GrassmannжөҒеҪўдёҠпјҢиҜҘжЁЎеһӢж—ЁеңЁеҗҢж—¶и§ЈеҶіи®Ўз®—ж•ҲзҺҮе’ҢеҸҜи§ЈйҮҠжҖ§дёӨеӨ§йҡҫйўҳгҖӮиҝҷдёҖжҖқжғізҡ„жҸҗеҮәпјҢж Үеҝ—зқҖеәҸеҲ—е»әжЁЎйўҶеҹҹејҖе§Ӣд»ҺвҖңжіЁж„ҸеҠӣдёӯеҝғи®әвҖқеҗ‘жӣҙеӨҡе…ғеҢ–зҡ„еҮ дҪ•ж–№жі•жҺўзҙўгҖӮ
3.1.1 жҸҗеҮәж— жіЁж„ҸеҠӣжңәеҲ¶зҡ„еәҸеҲ—жЁЎеһӢ
и®әж–ҮгҖҠAttention Is Not What You NeedгҖӢзҡ„ејҖзҜҮеҚіжҸҗеҮәдәҶдёҖдёӘж №жң¬жҖ§зҡ„й—®йўҳпјҡжҳҫејҸзҡ„LГ—LиҮӘжіЁж„ҸеҠӣжқғйҮҚеј йҮҸпјҢжҳҜеҗҰзңҹзҡ„жҳҜе®һзҺ°ејәеӨ§еәҸеҲ—е»әжЁЎе’ҢжҺЁзҗҶиғҪеҠӣжүҖеҝ…йңҖзҡ„ж №жң¬иҰҒзҙ пјҹ дҪңиҖ…зҡ„зӯ”жЎҲжҳҜвҖңеҗҰвҖқгҖӮ他们и®ӨдёәпјҢжіЁж„ҸеҠӣжңәеҲ¶еҸӘжҳҜе®һзҺ°йҡҗи—ҸиЎЁзӨәеҮ дҪ•жј”еҢ–зҡ„дёҖз§Қзү№е®ҡе®һзҺ°пјҢе…¶жҲҗеҠҹеңЁдәҺе®ғиғҪеӨҹжңүж•Ҳең°жҚ•жҚүtokenд№Ӣй—ҙзҡ„еӨҚжқӮе…ізі»пјҢдҪҶиҝҷз§ҚиғҪеҠӣеҸҜд»ҘйҖҡиҝҮе…¶д»–ж•°еӯҰе·Ҙе…·жқҘе®һзҺ°гҖӮдёәжӯӨпјҢ他们жҸҗеҮәдәҶдёҖз§Қе…Ёж–°зҡ„гҖҒе®Ңе…ЁдёҚеҢ…еҗ«жіЁж„ҸеҠӣзҹ©йҳөзҡ„еәҸеҲ—жЁЎеһӢпјҢеҚіеҹәдәҺGrassmannжөҒзҡ„жһ¶жһ„гҖӮиҜҘжЁЎеһӢзҡ„и®ҫи®Ўзӣ®ж ҮжҳҜпјҢеңЁдёҚдҪҝз”Ёд»»дҪ•жҳҫејҸжіЁж„ҸеҠӣжқғйҮҚзҡ„жғ…еҶөдёӢпјҢдҫқ然иғҪеӨҹиҫҫеҲ°дёҺTransformerзӣёеӘІзҫҺзҡ„жҖ§иғҪпјҢеҗҢж—¶д»Һж №жң¬дёҠж”№е–„жЁЎеһӢзҡ„и®Ўз®—ж•ҲзҺҮе’ҢеҸҜи§ЈйҮҠжҖ§гҖӮиҝҷдёҖжҸҗи®®жҳҜеҜ№зҺ°жңүTransformerиҢғејҸзҡ„дёҖж¬ЎеӨ§иғҶйқ©ж–°пјҢж—ЁеңЁе°Ҷз ”з©¶дәәе‘ҳзҡ„жіЁж„ҸеҠӣд»ҺвҖңеҰӮдҪ•дјҳеҢ–жіЁж„ҸеҠӣвҖқиҪ¬з§»еҲ°вҖңеҰӮдҪ•и®ҫи®Ўжӣҙдјҳзҡ„еҮ дҪ•жј”еҢ–жңәеҲ¶вҖқдёҠжқҘгҖӮ
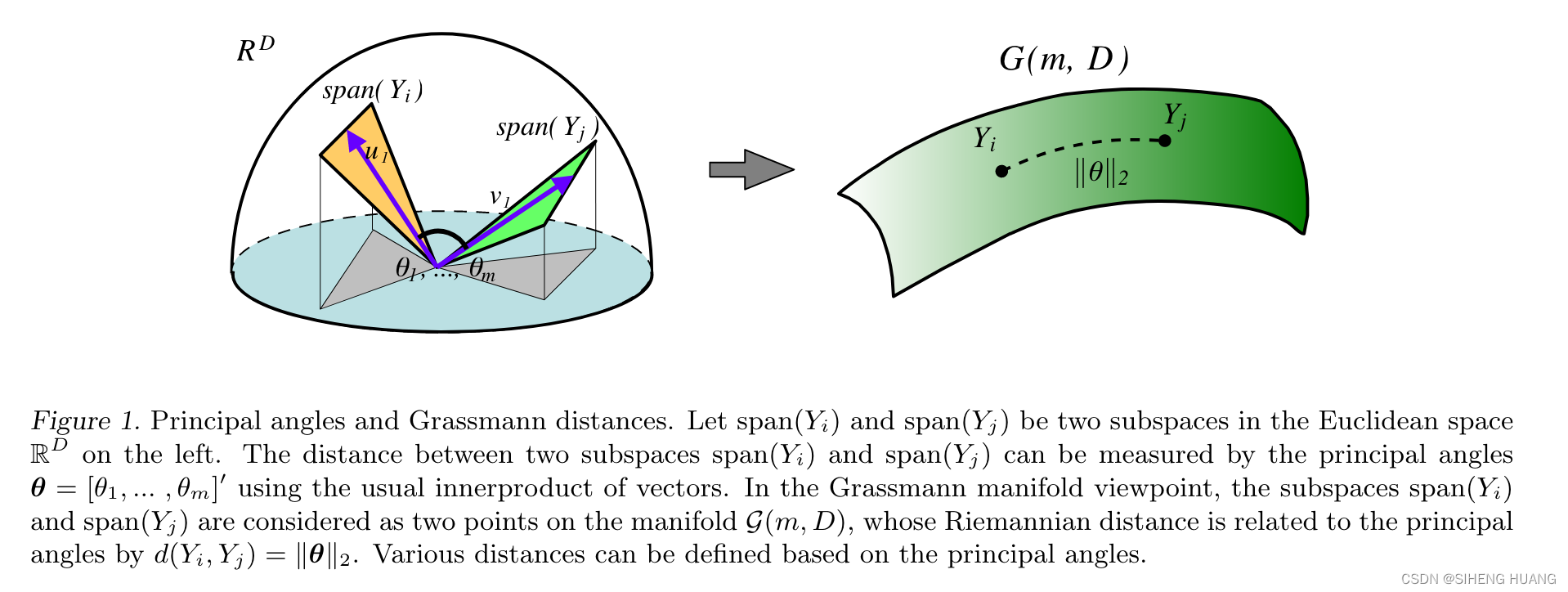
3.1.2 еҹәдәҺGrassmannжөҒеҪўзҡ„еҮ дҪ•ж–№жі•
Causal Grassmann Transformerзҡ„ж ёеҝғжҳҜеҹәдәҺGrassmannжөҒеҪўзҡ„еҮ дҪ•ж–№жі•гҖӮGrassmannжөҒеҪўGr(k, n)жҳҜжүҖжңүnз»ҙеҗ‘йҮҸз©әй—ҙдёӯkз»ҙеӯҗз©әй—ҙзҡ„йӣҶеҗҲгҖӮеңЁиҜҘжЁЎеһӢдёӯпјҢдҪңиҖ…е°Ҷtokenзҡ„йҡҗи—ҸзҠ¶жҖҒи§ЈйҮҠдёәжөҒеҪўдёҠзҡ„зӮ№пјҢ并йҖҡиҝҮжҺ§еҲ¶иҝҷдәӣеӯҗз©әй—ҙзҡ„еҪўеҸҳпјҲdeformationпјүжқҘе®һзҺ°дҝЎжҒҜзҡ„жөҒеҠЁе’ҢиһҚеҗҲгҖӮе…·дҪ“жқҘиҜҙпјҢжЁЎеһӢе°ҶжҜҸдёӘtokenзҡ„й«ҳз»ҙйҡҗи—ҸзҠ¶жҖҒеҗ‘йҮҸйҷҚз»ҙеҲ°дёҖдёӘиҫғдҪҺз»ҙеәҰзҡ„з©әй—ҙпјҢ然еҗҺйҖүеҸ–еәҸеҲ—дёӯзҡ„еұҖйғЁtokenеҜ№пјҢе°Ҷе®ғ们е…ұеҗҢеј жҲҗзҡ„дәҢз»ҙеӯҗз©әй—ҙи§ҶдёәGrassmannжөҒеҪўGr(2, r) дёҠзҡ„дёҖдёӘзӮ№гҖӮйҖҡиҝҮеңЁиҝҷдәӣдҪҺз»ҙеӯҗз©әй—ҙдёҠиҝӣиЎҢж“ҚдҪңпјҢжЁЎеһӢйҒҝе…ҚдәҶзӣҙжҺҘи®Ўз®—й«ҳз»ҙзҡ„LГ—LжіЁж„ҸеҠӣзҹ©йҳөгҖӮдҝЎжҒҜеңЁеәҸеҲ—дёӯзҡ„жөҒеҠЁдёҚеҶҚжҳҜдҫқиө–дәҺжҳҫејҸзҡ„жҲҗеҜ№жқғйҮҚпјҢиҖҢжҳҜйҖҡиҝҮи·ЁеұӮе’ҢеӨҡе°әеәҰеұҖйғЁзӘ—еҸЈеҜ№иҝҷдәӣдҪҺ秩еӯҗз©әй—ҙиҝӣиЎҢеҸ—жҺ§зҡ„еҮ дҪ•еҪўеҸҳжқҘе®һзҺ°зҡ„гҖӮиҝҷз§ҚеҹәдәҺжҳҺзЎ®еҮ дҪ•жөҒзҡ„ж“ҚдҪңпјҢдҪҝеҫ—жЁЎеһӢзҡ„ж ёеҝғжңәеҲ¶д»ҺдёҖдёӘйҡҫд»ҘеҲҶжһҗзҡ„вҖңй»‘зӣ’вҖқеј йҮҸз©әй—ҙпјҢиҪ¬з§»еҲ°дәҶдёҖдёӘж•°еӯҰдёҠз»“жһ„жё…жҷ°гҖҒжҖ§иҙЁжҳҺзЎ®зҡ„жөҒеҪўдёҠпјҢд»ҺиҖҢдёәжҸҗеҚҮжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§еҘ е®ҡдәҶеҹәзЎҖгҖӮ
3.2 жЁЎеһӢи®ҫи®ЎдёҺжңәеҲ¶
Causal Grassmann Transformerзҡ„жЁЎеһӢи®ҫи®ЎзІҫе·§ең°иһҚеҗҲдәҶйҷҚз»ҙгҖҒеҮ дҪ•еөҢе…Ҙе’Ңй—ЁжҺ§иһҚеҗҲзӯүжӯҘйӘӨпјҢеҪўжҲҗдәҶдёҖдёӘе®Ңе…ЁдёҚдҫқиө–жіЁж„ҸеҠӣзҹ©йҳөзҡ„и®Ўз®—жөҒзЁӢгҖӮиҜҘжңәеҲ¶йҖҡиҝҮе°ҶtokenеҜ№зҡ„е…ізі»иЎЁзӨәдёәGrassmannжөҒеҪўдёҠзҡ„еҮ дҪ•зү№еҫҒпјҢе®һзҺ°дәҶеҜ№еәҸеҲ—дҝЎжҒҜзҡ„жңүж•Ҳзј–з Ғе’ҢиһҚеҗҲпјҢеҗҢж—¶дҝқиҜҒдәҶи®Ўз®—зҡ„й«ҳж•ҲжҖ§гҖӮ
3.2.1 е°ҶTokenеҜ№и§ЈйҮҠдёәGrassmannжөҒеҪўдёҠзҡ„дәҢз»ҙеӯҗз©әй—ҙ
иҜҘжЁЎеһӢзҡ„е…ій”®еҲӣж–°еңЁдәҺе…¶еҜ№tokenй—ҙе…ізі»зҡ„иЎЁзӨәж–№ејҸгҖӮж ҮеҮҶTransformerйҖҡиҝҮи®Ўз®—дёӨдёӘtokenзҡ„жҹҘиҜўпјҲQueryпјүе’Ңй”®пјҲKeyпјүеҗ‘йҮҸзҡ„зӮ№з§ҜжқҘиЎЎйҮҸе®ғ们зҡ„зӣёдјјеәҰгҖӮиҖҢCausal Grassmann TransformerеҲҷйҮҮеҸ–дәҶдёҖз§ҚжҲӘ然дёҚеҗҢзҡ„еҮ дҪ•и§Ҷи§’гҖӮйҰ–е…ҲпјҢе®ғе°ҶжҜҸдёӘtokenзҡ„dз»ҙйҡҗи—ҸзҠ¶жҖҒеҗ‘йҮҸhtйҖҡиҝҮдёҖдёӘзәҝжҖ§еҸҳжҚўйҷҚз»ҙеҲ°дёҖдёӘrз»ҙзҡ„дҪҺз»ҙз©әй—ҙпјҢеҫ—еҲ°еҗ‘йҮҸzt вҲҲ R^rгҖӮ然еҗҺпјҢеҜ№дәҺеәҸеҲ—дёӯзҡ„дёҖдёӘеұҖйғЁзӘ—еҸЈеҶ…зҡ„tokenеҜ№пјҲдҫӢеҰӮпјҢдҪҚзҪ®iе’Ңjзҡ„tokenпјүпјҢжЁЎеһӢе°ҶиҝҷдёӨдёӘtokenеҜ№еә”зҡ„дҪҺз»ҙеҗ‘йҮҸziе’ҢzjзңӢдҪңжҳҜеј жҲҗдёҖдёӘдәҢз»ҙеӯҗз©әй—ҙзҡ„еҹәзЎҖгҖӮиҝҷдёӘдәҢз»ҙеӯҗз©әй—ҙжң¬иә«е°ұжҳҜGrassmannжөҒеҪўGr(2, r)дёҠзҡ„дёҖдёӘзӮ№гҖӮйҖҡиҝҮиҝҷз§Қж–№ејҸпјҢжЁЎеһӢе°ҶtokenеҜ№зҡ„иҜӯд№үе…ізі»зј–з ҒдёәдәҶдёҖдёӘжҳҺзЎ®зҡ„еҮ дҪ•еҜ№иұЎгҖӮиҝҷз§ҚиЎЁзӨәж–№ејҸзҡ„дјҳеҠҝеңЁдәҺпјҢе®ғе°ҶеӨҚжқӮзҡ„гҖҒй«ҳз»ҙзҡ„еҗ‘йҮҸе…ізі»иҪ¬еҢ–дёәдёҖдёӘеңЁж•°еӯҰдёҠжҖ§иҙЁиүҜеҘҪгҖҒжҳ“дәҺж“ҚдҪңзҡ„еҮ дҪ•е®һдҪ“пјҢдёәеҗҺз»ӯзҡ„зү№еҫҒжҸҗеҸ–е’ҢдҝЎжҒҜиһҚеҗҲеҘ е®ҡдәҶеҹәзЎҖгҖӮ
3.2.2 йҖҡиҝҮйҷҚдҪҺTokenз»ҙеәҰе®һзҺ°еҸҜи§ЈйҮҠжҖ§
йҖҡиҝҮе°ҶtokenзҠ¶жҖҒйҷҚз»ҙеҲ°дҪҺз»ҙз©әй—ҙеҶҚиҝӣиЎҢеҮ дҪ•ж“ҚдҪңпјҢCausal Grassmann TransformerеңЁи®ҫи®ЎдёҠе°ұжҸҗеҚҮдәҶжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§гҖӮдёҺеңЁй«ҳз»ҙdз»ҙз©әй—ҙдёӯзӣҙжҺҘж“ҚдҪңзӣёжҜ”пјҢеңЁдёҖдёӘеҸҜжҺ§зҡ„rз»ҙпјҲr << dпјүз©әй—ҙдёӯеҲҶжһҗеӯҗз©әй—ҙзҡ„еҪўеҸҳиҰҒе®№жҳ“еҫ—еӨҡгҖӮжЁЎеһӢдёҚеҶҚдҫқиө–дәҺдёҖдёӘеҢ…еҗ«LВІдёӘиҮӘз”ұеҸӮж•°зҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҢиҖҢжҳҜйҖҡиҝҮдёҖзі»еҲ—еңЁGr(2, r)жөҒеҪўдёҠзҡ„ж“ҚдҪңжқҘжј”еҢ–дҝЎжҒҜгҖӮиҝҷз§ҚдҪҺз»ҙеҮ дҪ•жј”еҢ–жңәеҲ¶дҪҝеҫ—иҝҪиёӘдҝЎжҒҜеңЁжЁЎеһӢдёӯзҡ„жөҒеҠЁи·Ҝеҫ„жҲҗдёәеҸҜиғҪгҖӮжҲ‘们еҸҜд»ҘеҲҶжһҗеңЁжҜҸдёҖеұӮдёӯпјҢе“ӘдәӣtokenеҜ№зҡ„еӯҗз©әй—ҙеҸ‘з”ҹдәҶжҳҫи‘—еҸҳеҢ–пјҢд»ҘеҸҠиҝҷдәӣеҸҳеҢ–еҰӮдҪ•еҪұе“ҚжңҖз»Ҳзҡ„иҫ“еҮәгҖӮиҝҷз§ҚеҹәдәҺжҳҺзЎ®еҮ дҪ•еҸҳжҚўзҡ„жЁЎеһӢж ёеҝғпјҢзӣёжҜ”дәҺй«ҳз»ҙеј йҮҸз©әй—ҙдёӯеӨҚжқӮзҡ„гҖҒйқһзәҝжҖ§зҡ„зӣёдә’дҪңз”ЁпјҢжӣҙе®№жҳ“иў«ж•°еӯҰе·Ҙе…·жүҖеҲҶжһҗпјҢд»ҺиҖҢжңүжңӣжү“з ҙеӨ§еһӢTransformerжЁЎеһӢзҡ„вҖңй»‘зӣ’вҖқеӣ°еўғгҖӮдҪңиҖ…и®ӨдёәпјҢиҝҷз§Қд»Һ вҖңй«ҳз»ҙеј йҮҸжҸҗеҚҮвҖқеҲ°вҖңдҪҺз»ҙеҮ дҪ•жј”еҢ–вҖқ зҡ„иҪ¬еҸҳпјҢжҳҜи§ЈеҶіжЁЎеһӢдёҚеҸҜи§ЈйҮҠжҖ§й—®йўҳзҡ„е…ій”®жүҖеңЁгҖӮ
3.2.3 дёҚдҫқиө–жҳҫејҸжіЁж„ҸеҠӣзҹ©йҳөзҡ„и®Ўз®—жөҒзЁӢ
Causal Grassmann Transformerзҡ„и®Ўз®—жөҒзЁӢе®Ңе…Ёж‘’ејғдәҶжҳҫејҸзҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҢе…¶е…·дҪ“жӯҘйӘӨеҰӮдёӢпјҡ
- йҷҚз»ҙпјҲDimensionality Reductionпјү пјҡйҰ–е…ҲпјҢе°Ҷиҫ“е…ҘеәҸеҲ—зҡ„жҜҸдёӘtokenзҡ„dз»ҙйҡҗи—ҸзҠ¶жҖҒhtйҖҡиҝҮдёҖдёӘеҸҜеӯҰд№ зҡ„зәҝжҖ§еҸҳжҚўWdown вҲҲ R^(dГ—r)жҠ•еҪұеҲ°дёҖдёӘrз»ҙзҡ„дҪҺз»ҙз©әй—ҙпјҢеҫ—еҲ°zt = ht WdownгҖӮ
- еӯҗз©әй—ҙжһ„е»әпјҲSubspace Constructionпјү пјҡеңЁдёҖдёӘеұҖйғЁзҡ„гҖҒеӣ жһңжҖ§зҡ„зӘ—еҸЈеҶ…пјҲдҫӢеҰӮпјҢеҜ№дәҺдҪҚзҪ®tзҡ„tokenпјҢиҖғиҷ‘е…¶еүҚkдёӘtokenпјүпјҢйҖүеҸ–tokenеҜ№пјҲt, jпјүпјҢе…¶дёӯj вҲҲ [t-k, t-1]гҖӮе°ҶеҜ№еә”зҡ„дҪҺз»ҙеҗ‘йҮҸztе’Ңzjз»„еҗҲиө·жқҘпјҢеҪўжҲҗдёҖдёӘ2Г—rзҡ„зҹ©йҳөгҖӮиҝҷдёӘзҹ©йҳөзҡ„иЎҢз©әй—ҙе®ҡд№үдәҶGr(2, r)дёҠзҡ„дёҖдёӘдәҢз»ҙеӯҗз©әй—ҙгҖӮ
- PlГјckerеөҢе…ҘпјҲPlГјcker Embeddingпјү пјҡдёәдәҶеңЁзҘһз»ҸзҪ‘з»ңдёӯж–№дҫҝең°иЎЁзӨәе’Ңж“ҚдҪңиҝҷдәӣеӯҗз©әй—ҙпјҢжЁЎеһӢдҪҝз”ЁдәҶPlГјckerеқҗж ҮгҖӮPlГјckerеқҗж ҮжҳҜдёҖз§Қе°ҶGr(k, n)дёҠзҡ„зӮ№еөҢе…ҘеҲ°жӣҙй«ҳз»ҙеәҰзҡ„е°„еҪұз©әй—ҙзҡ„ж–№жі•гҖӮеҜ№дәҺдәҢз»ҙеӯҗз©әй—ҙпјҢе…¶PlГјckerеқҗж ҮеҸҜд»ҘйҖҡиҝҮеҜ№2Г—rзҹ©йҳөзҡ„дёӨиЎҢиҝӣиЎҢеӨ–з§Ҝиҝҗз®—еҫ—еҲ°пјҢз»“жһңжҳҜдёҖдёӘеҸҚеҜ№з§°зҡ„rГ—rзҹ©йҳөгҖӮиҝҷдёӘзҹ©йҳөеҸҜд»Ҙиў«еұ•е№іпјҲflattenпјүжҲҗдёҖдёӘй•ҝеәҰдёәr(r-1)/2зҡ„еҗ‘йҮҸпјҢиҝҷдёӘеҗ‘йҮҸе°ұжҳҜиҜҘеӯҗз©әй—ҙеңЁPlГјckerеөҢе…ҘдёӢзҡ„иЎЁзӨәгҖӮиҝҷдёӘеөҢе…ҘиҝҮзЁӢжҳҜеҸҜеҫ®зҡ„пјҢеӣ жӯӨеҸҜд»Ҙж— зјқйӣҶжҲҗеҲ°з«ҜеҲ°з«Ҝзҡ„зҘһз»ҸзҪ‘з»ңи®ӯз»ғдёӯгҖӮ
- зү№еҫҒиһҚеҗҲпјҲFeature Fusionпјү пјҡе°ҶPlГјckerеөҢе…Ҙеҫ—еҲ°зҡ„еҮ дҪ•зү№еҫҒеҗ‘йҮҸйҖҡиҝҮдёҖдёӘй—ЁжҺ§ж··еҗҲеқ—пјҲgated mixing blockпјү иһҚеҗҲеӣһеҺҹе§Ӣзҡ„йҡҗи—ҸзҠ¶жҖҒh_tгҖӮиҝҷдёӘй—ЁжҺ§жңәеҲ¶е…Ғи®ёжЁЎеһӢйҖүжӢ©жҖ§ең°еҗёж”¶д»ҺеұҖйғЁеҮ дҪ•з»“жһ„дёӯжҸҗеҸ–зҡ„дҝЎжҒҜпјҢд»ҺиҖҢжӣҙж–°tokenзҡ„иЎЁзӨәгҖӮ
йҖҡиҝҮиҝҷдёҖзі»еҲ—ж“ҚдҪңпјҢжЁЎеһӢе®һзҺ°дәҶдҝЎжҒҜзҡ„жөҒеҠЁе’ҢиһҚеҗҲпјҢиҖҢж•ҙдёӘиҝҮзЁӢзҡ„и®Ўз®—еӨҚжқӮеәҰдёҺеәҸеҲ—й•ҝеәҰLе’Ңеӯҗз©әй—ҙз»ҙеәҰrзӣёе…іпјҢйҒҝе…ҚдәҶO(LВІd)зҡ„дәҢ次方瓶йўҲгҖӮ
3.3 еӨҚжқӮеәҰдёҺжҖ§иғҪеҲҶжһҗ
Causal Grassmann TransformerеңЁзҗҶи®әеӨҚжқӮеәҰе’Ңе®һйҷ…жҖ§иғҪдёҠйғҪеұ•зҺ°еҮәдәҶдҪңдёәTransformerжӣҝд»Јж–№жЎҲзҡ„жҪңеҠӣгҖӮе…¶зәҝжҖ§еӨҚжқӮеәҰзҡ„зү№жҖ§дҪҝе…¶еңЁеӨ„зҗҶй•ҝеәҸеҲ—ж—¶е…·жңүеӨ©з„¶дјҳеҠҝпјҢиҖҢе®һйӘҢз»“жһңд№ҹеҲқжӯҘйӘҢиҜҒдәҶе…¶еңЁзү№е®ҡд»»еҠЎдёҠиҫҫеҲ°дёҺTransformerзӣёеҪ“з”ҡиҮіз•ҘдјҳжҖ§иғҪзҡ„иғҪеҠӣгҖӮ
3.3.1 зәҝжҖ§еӨҚжқӮеәҰпјҡеңЁеӣәе®ҡ秩дёӢйҡҸеәҸеҲ—й•ҝеәҰзәҝжҖ§еўһй•ҝ
иҜҘжЁЎеһӢжңҖеј•дәәжіЁзӣ®зҡ„дјҳеҠҝд№ӢдёҖжҳҜе…¶и®Ўз®—еӨҚжқӮеәҰгҖӮи®әж–Үдёӯзҡ„еӨҚжқӮеәҰеҲҶжһҗиЎЁжҳҺпјҢе…¶ж ёеҝғзҡ„ж··еҗҲжңәеҲ¶пјҲmixing mechanismпјүеңЁеӣәе®ҡеӯҗз©әй—ҙ秩rзҡ„жғ…еҶөдёӢпјҢи®Ўз®—еӨҚжқӮеәҰйҡҸеәҸеҲ—й•ҝеәҰLзәҝжҖ§еўһй•ҝгҖӮжҲ‘们жқҘиҜҰз»ҶеҲҶжһҗе…¶и®Ўз®—иҝҮзЁӢпјҡ
- йҷҚз»ҙпјҡе°ҶLдёӘdз»ҙеҗ‘йҮҸйҷҚз»ҙеҲ°rз»ҙпјҢеӨҚжқӮеәҰдёәO(L d r)гҖӮ
- еӯҗз©әй—ҙжһ„е»әдёҺPlГјckerеөҢе…ҘпјҡеҜ№дәҺжҜҸдёӘдҪҚзҪ®tпјҢжЁЎеһӢеңЁдёҖдёӘеӨ§е°Ҹдёәkзҡ„еұҖйғЁзӘ—еҸЈеҶ…еӨ„зҗҶkдёӘtokenеҜ№гҖӮжҜҸдёӘtokenеҜ№зҡ„PlГјckerеөҢе…Ҙж“ҚдҪңпјҲдё»иҰҒжҳҜеӨ–з§Ҝе’Ңеұ•е№іпјүзҡ„еӨҚжқӮеәҰжҳҜO(rВІ)гҖӮеӣ жӯӨпјҢеҜ№дәҺж•ҙдёӘй•ҝеәҰдёәLзҡ„еәҸеҲ—пјҢиҝҷдёҖжӯҘзҡ„жҖ»еӨҚжқӮеәҰжҳҜO(L k rВІ)гҖӮз”ұдәҺkйҖҡеёёжҳҜдёҖдёӘиҝңе°ҸдәҺLзҡ„еёёж•°пјҢиҝҷдёӘеӨҚжқӮеәҰеҸҜд»ҘзңӢдҪңжҳҜO(L rВІ)гҖӮ
- зү№еҫҒиһҚеҗҲпјҡе°ҶPlГјckerзү№еҫҒиһҚеҗҲеӣһйҡҗи—ҸзҠ¶жҖҒпјҢе…¶еӨҚжқӮеәҰдёҺйҡҗи—ҸзҠ¶жҖҒз»ҙеәҰdе’ҢPlГјckerзү№еҫҒз»ҙеәҰпјҲзәҰдёәrВІпјүзӣёе…іпјҢжҖ»еӨҚжқӮеәҰдёәO(L d rВІ)гҖӮ
з»јеҗҲжқҘзңӢпјҢж•ҙдёӘжЁЎеһӢзҡ„и®Ўз®—еӨҚжқӮеәҰдё»иҰҒз”ұO(L
d r)е’ҢO(L
d rВІ)еҶіе®ҡгҖӮз”ұдәҺrжҳҜдёҖдёӘеӣәе®ҡзҡ„гҖҒиҝңе°ҸдәҺdе’ҢLзҡ„и¶…еҸӮж•°пјҢеӣ жӯӨжЁЎеһӢзҡ„ж•ҙдҪ“еӨҚжқӮеәҰжҳҜ
зәҝжҖ§зҡ„пјҢеҚіO(L) гҖӮиҝҷдёҺж ҮеҮҶTransformerзҡ„O(LВІd)еӨҚжқӮеәҰеҪўжҲҗдәҶйІңжҳҺеҜ№жҜ”пјҢдҪҝеҫ—Causal Grassmann TransformerеңЁеӨ„зҗҶй•ҝеәҸеҲ—ж—¶е…·жңүе·ЁеӨ§зҡ„и®Ўз®—дјҳеҠҝгҖӮ
3.3.2 е®һйӘҢз»“жһңпјҡеңЁWikitext-2е’ҢSNLIж•°жҚ®йӣҶдёҠзҡ„иЎЁзҺ°
и®әж–ҮеңЁдёӨдёӘз»Ҹе…ёзҡ„NLPд»»еҠЎдёҠеҜ№Causal Grassmann TransformerиҝӣиЎҢдәҶиҜ„дј°пјҢд»ҘйӘҢиҜҒе…¶жңүж•ҲжҖ§гҖӮ
- иҜӯиЁҖе»әжЁЎпјҲLanguage Modelingпјү пјҡеңЁWikitext-2ж•°жҚ®йӣҶдёҠпјҢдҪңиҖ…и®ӯз»ғдәҶдёҖдёӘзәҜзІ№зҡ„гҖҒеҹәдәҺGrassmannзҡ„иҜӯиЁҖжЁЎеһӢгҖӮиҜҘжЁЎеһӢеҢ…еҗ«13-18MдёӘеҸӮж•°гҖӮе®һйӘҢз»“жһңжҳҫзӨәпјҢе…¶йӘҢиҜҒйӣҶдёҠзҡ„еӣ°жғ‘еәҰпјҲperplexityпјүдёҺдёҖдёӘеҸӮж•°йҮҸзӣёеҢ№й…Қзҡ„TransformerеҹәзәҝжЁЎеһӢзӣёжҜ”пјҢе·®и·қеңЁ10-15%д»ҘеҶ…гҖӮиҝҷдёӘз»“жһңйқһеёёйҮҚиҰҒпјҢеӣ дёәе®ғзӣҙжҺҘиҜҒжҳҺдәҶе®Ңе…ЁдёҚдҪҝз”ЁжіЁж„ҸеҠӣжңәеҲ¶пјҢд»…еҮӯеҮ дҪ•жөҒж“ҚдҪңпјҢд№ҹиғҪеӨҹеӯҰд№ еҲ°ејәеӨ§зҡ„иҜӯиЁҖжЁЎеһӢпјҢ并且жҖ§иғҪеҸҜд»ҘжҺҘиҝ‘дёҡз•Ңж ҮеҮҶгҖӮ
- иҮӘ然иҜӯиЁҖжҺЁзҗҶпјҲNatural Language Inferenceпјү пјҡеңЁSNLIж•°жҚ®йӣҶдёҠпјҢдҪңиҖ…е°ҶGrassmann-basedзҡ„еҲҶзұ»еӨҙпјҲclassification headпјүжҺҘеңЁйў„и®ӯз»ғзҡ„DistilBERTзј–з ҒеҷЁд№ӢеҗҺпјҢд»Ҙжӣҝд»ЈеҺҹжңүзҡ„TransformerеҲҶзұ»еӨҙгҖӮе®һйӘҢз»“жһңиЎЁжҳҺпјҢGrassmannеҲҶзұ»еӨҙеңЁйӘҢиҜҒйӣҶдёҠзҡ„жңҖдҪіеҮҶзЎ®зҺҮиҫҫеҲ°дәҶ0.8550пјҢз•Ҙй«ҳдәҺTransformerеҲҶзұ»еӨҙзҡ„0.8545пјӣеңЁжөӢиҜ•йӣҶдёҠзҡ„еҮҶзЎ®зҺҮд№ҹиҫҫеҲ°дәҶ0.8538пјҢдјҳдәҺTransformerзҡ„0.8511гҖӮиҝҷдёӘе®һйӘҢиЎЁжҳҺпјҢGrassmannжңәеҲ¶дёҚд»…йҖӮз”ЁдәҺиҜӯиЁҖе»әжЁЎпјҢд№ҹиғҪеңЁйңҖиҰҒеӨҚжқӮиҜӯд№үзҗҶи§Јзҡ„дёӢжёёд»»еҠЎдёӯеҸ‘жҢҘдҪңз”ЁпјҢ并且еҸҜиғҪе…·жңүдёҖдәӣзӢ¬зү№зҡ„дјҳеҠҝгҖӮ
3.3.3 дёҺж ҮеҮҶTransformerзҡ„жҖ§иғҪеҜ№жҜ”
дёәдәҶжӣҙжё…жҷ°ең°еұ•зӨәCausal Grassmann Transformerзҡ„жҖ§иғҪпјҢжҲ‘们еҸҜд»Ҙе°Ҷе…¶е®һйӘҢз»“жһңдёҺж ҮеҮҶTransformerиҝӣиЎҢеҜ№жҜ”жҖ»з»“гҖӮ
| д»»еҠЎ | ж•°жҚ®йӣҶ | жЁЎеһӢ | еҸӮж•°йҮҸ | жҖ§иғҪжҢҮж Ү | з»“жһң | еҜ№жҜ” |
|---|
| **иҜӯиЁҖе»әжЁЎ** | Wikitext-2 | Causal Grassmann LM | 13-18M | йӘҢиҜҒйӣҶеӣ°жғ‘еәҰ | дёҺTransformerеҹәзәҝе·®и·қеңЁ10-15%д»ҘеҶ… | жҖ§иғҪжҺҘиҝ‘пјҢиҜҒжҳҺдәҶж— жіЁж„ҸеҠӣжЁЎеһӢзҡ„еҸҜиЎҢжҖ§ |
| **иҮӘ然иҜӯиЁҖжҺЁзҗҶ** | SNLI | DistilBERT + Grassmann Head | - | йӘҢиҜҒйӣҶеҮҶзЎ®зҺҮ | **0.8550** | **дјҳдәҺ** Transformer Head (0.8545) |
| | DistilBERT + Grassmann Head | - | жөӢиҜ•йӣҶеҮҶзЎ®зҺҮ | **0.8538** | **дјҳдәҺ** Transformer Head (0.8511) |
д»ҺдёҠиЎЁеҸҜд»ҘзңӢеҮәпјҢCausal Grassmann TransformerеңЁдҝқжҢҒиҝңдҪҺдәҺTransformerзҡ„и®Ўз®—еӨҚжқӮеәҰзҡ„еҗҢж—¶пјҢеңЁжҖ§иғҪдёҠеұ•зҺ°еҮәдәҶејәеӨ§зҡ„з«һдәүеҠӣгҖӮе°Өе…¶жҳҜеңЁSNLIд»»еҠЎдёҠпјҢе®ғз”ҡиҮіеҸ–еҫ—дәҶжҜ”ж ҮеҮҶTransformerеҲҶзұ»еӨҙжӣҙеҘҪзҡ„з»“жһңпјҢиҝҷеҸҜиғҪжҡ—зӨәдәҶеҹәдәҺеҮ дҪ•зҡ„иЎЁзӨәж–№жі•еңЁжҚ•жҚүеҸҘеӯҗеҜ№д№Ӣй—ҙзҡ„з»Ҷеҫ®иҜӯд№үе…ізі»ж–№йқўе…·жңүзӢ¬зү№зҡ„дјҳеҠҝгҖӮиҝҷдәӣеҲқжӯҘзҡ„е®һйӘҢз»“жһңжңүеҠӣең°ж”ҜжҢҒдәҶи®әж–Үзҡ„ж ёеҝғи§ӮзӮ№пјҡеҚідёҖдёӘи®ҫи®ЎиүҜеҘҪзҡ„еҮ дҪ•жј”еҢ–жңәеҲ¶пјҢеҸҜд»ҘеңЁдёҚдҫқиө–жіЁж„ҸеҠӣзҡ„жғ…еҶөдёӢпјҢе®һзҺ°ејәеӨ§зҡ„еәҸеҲ—е»әжЁЎиғҪеҠӣгҖӮ
4. з»“и®әдёҺеұ•жңӣ
йҖҡиҝҮеҜ№и®әж–ҮгҖҠAttention Is All You NeedгҖӢдёӯL2е№іж–№еӨҚжқӮеәҰе’ҢвҖңй»‘зӣ’вҖқй—®йўҳзҡ„ж·ұе…Ҙеү–жһҗпјҢд»ҘеҸҠеҜ№зҺ°жңүжӣҝд»Јж–№жЎҲзҡ„з»јиҝ°пјҢжҲ‘们еҸҜд»Ҙжё…жҷ°ең°зңӢеҲ°пјҢTransformerжһ¶жһ„зҡ„жј”иҝӣжӯЈжңқзқҖжӣҙй«ҳж•ҲгҖҒжӣҙйҖҸжҳҺзҡ„ж–№еҗ‘еҸ‘еұ•гҖӮеңЁиҝҷдёҖиғҢжҷҜдёӢпјҢи®әж–ҮгҖҠAttention Is Not What You NeedгҖӢжҸҗеҮәзҡ„Causal Grassmann TransformerжЁЎеһӢпјҢд»Ҙе…¶зӢ¬зү№зҡ„еҮ дҪ•и§Ҷи§’е’ҢеҲӣж–°зҡ„ж— жіЁж„ҸеҠӣи®ҫи®ЎпјҢдёәжҲ‘们жҸҗдҫӣдәҶдёҖдёӘжһҒе…·жҪңеҠӣзҡ„з»јеҗҲи§ЈеҶіж–№жЎҲгҖӮ
4.1 Causal Grassmann TransformerдҪңдёәз»јеҗҲи§ЈеҶіж–№жЎҲзҡ„жҪңеҠӣ
Causal Grassmann TransformerжңҖеј•дәәжіЁзӣ®зҡ„ең°ж–№еңЁдәҺпјҢе®ғ并йқһд»…д»…й’ҲеҜ№L2еӨҚжқӮеәҰжҲ–вҖңй»‘зӣ’вҖқй—®йўҳдёӯзҡ„жҹҗдёҖдёӘиҝӣиЎҢдјҳеҢ–пјҢиҖҢжҳҜиҜ•еӣҫйҖҡиҝҮдёҖдёӘз»ҹдёҖзҡ„жЎҶжһ¶жқҘеҗҢж—¶и§ЈеҶіиҝҷдёӨдёӘж ёеҝғжҢ‘жҲҳгҖӮ
4.1.1 еҗҢж—¶и§ЈеҶіеӨҚжқӮеәҰе’ҢеҸҜи§ЈйҮҠжҖ§й—®йўҳ
иҜҘжЁЎеһӢйҖҡиҝҮе°ҶtokenдәӨдә’д»Һи®Ўз®—жҳӮиҙөзҡ„зҹ©йҳөд»Јж•°иҪ¬жҚўеҲ°еҮ дҪ•ж„Ҹд№үжҳҺзЎ®зҡ„GrassmannжөҒеҪўдёҠпјҢе®һзҺ°дәҶеҸҢйҮҚзӘҒз ҙгҖӮдёҖж–№йқўпјҢе®ғйҖҡиҝҮйҒҝе…ҚжҳҫејҸи®Ўз®—nГ—nзҡ„жіЁж„ҸеҠӣзҹ©йҳөпјҢе°Ҷи®Ўз®—еӨҚжқӮеәҰд»ҺдәҢж¬Ўж–№йҷҚдҪҺеҲ°зәҝжҖ§пјҢжһҒеӨ§ең°жҸҗеҚҮдәҶжЁЎеһӢеӨ„зҗҶй•ҝеәҸеҲ—зҡ„ж•ҲзҺҮе’ҢеҸҜиЎҢжҖ§гҖӮеҸҰдёҖж–№йқўпјҢе®ғе°ҶжЁЎеһӢзҡ„ж ёеҝғж“ҚдҪңе»әз«ӢеңЁе…·жңүжҳҺзЎ®ж•°еӯҰз»“жһ„зҡ„жөҒеҪўдёҠпјҢдҪҝеҫ—дҝЎжҒҜжөҒеҠЁеҸҜд»ҘйҖҡиҝҮеӯҗз©әй—ҙзҡ„жј”еҢ–жқҘиҝҪиёӘе’ҢеҲҶжһҗпјҢд»ҺиҖҢеҶ…еңЁең°жҸҗеҚҮдәҶжЁЎеһӢзҡ„еҸҜи§ЈйҮҠжҖ§гҖӮиҝҷз§ҚвҖңдёҖзҹідәҢйёҹвҖқзҡ„и®ҫи®ЎжҖқи·ҜпјҢдҪҝе…¶еңЁдј—еӨҡдјҳеҢ–ж–№жЎҲдёӯи„ұйў–иҖҢеҮәпјҢеұ•зӨәдәҶд»Һж №жң¬дёҠйҮҚеЎ‘еәҸеҲ—е»әжЁЎжһ¶жһ„зҡ„жҪңеҠӣгҖӮ
4.1.2 жЁЎеһӢеңЁзү№е®ҡд»»еҠЎдёҠзҡ„дјҳеҠҝдёҺеұҖйҷҗжҖ§
е°Ҫз®ЎCausal Grassmann Transformerеұ•зҺ°дәҶе·ЁеӨ§зҡ„жҪңеҠӣпјҢдҪҶжҲ‘们д№ҹеҝ…йЎ»жё…йҶ’ең°и®ӨиҜҶеҲ°е…¶еҪ“еүҚзҡ„дјҳеҠҝдёҺеұҖйҷҗжҖ§гҖӮеңЁдјҳеҠҝж–№йқўпјҢйҷӨдәҶзәҝжҖ§зҡ„еӨҚжқӮеәҰе’ҢжӣҙеҘҪзҡ„еҸҜи§ЈйҮҠжҖ§пјҢиҜҘжЁЎеһӢеңЁSNLIзӯүйңҖиҰҒзІҫз»ҶзҗҶи§ЈеҸҘеӯҗй—ҙе…ізі»зҡ„д»»еҠЎдёҠз”ҡиҮіиЎЁзҺ°еҮәдјҳдәҺж ҮеҮҶTransformerзҡ„жҪңеҠӣпјҢиҝҷжҡ—зӨәдәҶGrassmannжөҒеҪўдёҠзҡ„еҮ дҪ•ж“ҚдҪңеңЁжҚ•жҚүз»“жһ„еҢ–дҝЎжҒҜж–№йқўеҸҜиғҪе…·жңүзӢ¬зү№зҡ„дјҳеҠҝгҖӮ然иҖҢпјҢе…¶еұҖйҷҗжҖ§д№ҹеҗҢж ·жҳҺжҳҫгҖӮеңЁиҜӯиЁҖе»әжЁЎд»»еҠЎдёҠпјҢе…¶жҖ§иғҪдёҺйЎ¶е°–зҡ„TransformerжЁЎеһӢзӣёжҜ”д»Қжңүе·®и·қгҖӮжӯӨеӨ–пјҢдҪңдёәдёҖз§Қж–°е…ҙзҡ„жһ¶жһ„пјҢе…¶и®ӯз»ғзЁіе®ҡжҖ§гҖҒжіӣеҢ–иғҪеҠӣд»ҘеҸҠеңЁжӣҙе№ҝжіӣд»»еҠЎпјҲеҰӮжңәеҷЁзҝ»иҜ‘гҖҒеӨҡжЁЎжҖҒеӯҰд№ пјүдёҠзҡ„иЎЁзҺ°д»Қжңүеҫ…иҝӣдёҖжӯҘйӘҢиҜҒгҖӮжЁЎеһӢзҡ„е®һзҺ°е’Ңи°ғдјҳеҸҜиғҪжҜ”ж ҮеҮҶзҡ„Transformerжӣҙе…·жҢ‘жҲҳжҖ§пјҢеӣ дёәе®ғж¶үеҸҠеҲ°еҮ дҪ•жҰӮеҝөдёҺж·ұеәҰеӯҰд№ жЎҶжһ¶зҡ„ж·ұеәҰиһҚеҗҲгҖӮ
4.2 жңӘжқҘз ”з©¶ж–№еҗ‘
Causal Grassmann Transformerзҡ„еҮәзҺ°пјҢдёәжңӘжқҘзҡ„з ”з©¶ејҖиҫҹдәҶеӨҡдёӘе……ж»ЎеүҚжҷҜзҡ„ж–№еҗ‘гҖӮ
4.2.1 ж— жіЁж„ҸеҠӣжңәеҲ¶жЁЎеһӢзҡ„иҝӣдёҖжӯҘеҸ‘еұ•
иҜҘжЁЎеһӢзҡ„жҲҗеҠҹиҜҒжҳҺдәҶ вҖңж— жіЁж„ҸеҠӣвҖқеәҸеҲ—е»әжЁЎзҡ„еҸҜиЎҢжҖ§пјҢиҝҷе°ҶжҝҖеҠұжӣҙеӨҡз ”з©¶иҖ…и·іеҮәжіЁж„ҸеҠӣжңәеҲ¶зҡ„жЎҶжһ¶пјҢжҺўзҙўе…¶д»–ж–°йў–зҡ„еәҸеҲ—дәӨдә’иҢғејҸгҖӮжңӘжқҘзҡ„з ”з©¶еҸҜд»ҘжҺўзҙўдёҚеҗҢзҡ„еҮ дҪ•жөҒеҪўгҖҒдёҚеҗҢзҡ„еӯҗз©әй—ҙиЎЁзӨәж–№жі•пјҢжҲ–иҖ…е°ҶеҮ дҪ•ж·ұеәҰеӯҰд№ дёҺе…¶д»–жҠҖжңҜпјҲеҰӮзҠ¶жҖҒз©әй—ҙжЁЎеһӢпјүзӣёз»“еҗҲпјҢд»Ҙжһ„е»әжӣҙй«ҳж•ҲгҖҒжӣҙејәеӨ§зҡ„ж— жіЁж„ҸеҠӣжһ¶жһ„гҖӮиҝҷеҸҜиғҪдјҡеӮ¬з”ҹдёҖдёӘе…Ёж–°зҡ„жЁЎеһӢ家ж—ҸпјҢдёҺеҹәдәҺжіЁж„ҸеҠӣзҡ„TransformerеҪўжҲҗдә’иЎҘжҲ–з«һдәүгҖӮ
4.2.2 еҮ дҪ•ж·ұеәҰеӯҰд№ еңЁеәҸеҲ—е»әжЁЎдёӯзҡ„еә”з”ЁеүҚжҷҜ
Causal Grassmann TransformerжҳҜеҮ дҪ•ж·ұеәҰеӯҰд№ пјҲGeometric Deep Learningпјү жҖқжғіеңЁеәҸеҲ—е»әжЁЎйўҶеҹҹзҡ„дёҖж¬ЎжҲҗеҠҹеә”з”ЁгҖӮиҝҷдёәе°Ҷе…¶д»–еҮ дҪ•е’ҢжӢ“жү‘е·Ҙе…·еј•е…Ҙж·ұеәҰеӯҰд№ жҸҗдҫӣдәҶиҢғдҫӢгҖӮжңӘжқҘзҡ„з ”з©¶еҸҜд»ҘжҺўзҙўеҰӮдҪ•еҲ©з”ЁжӣҙеӨҚжқӮзҡ„еҮ дҪ•з»“жһ„пјҲеҰӮжқҺзҫӨгҖҒеӣҫжөҒеҪўпјүжқҘи®ҫи®ЎзҘһз»ҸзҪ‘з»ңеұӮпјҢжҲ–иҖ…еҰӮдҪ•еҲ©з”ЁжӢ“жү‘ж•°жҚ®еҲҶжһҗпјҲTDAпјүзҡ„ж–№жі•жқҘзҗҶи§Је’ҢеҲҶжһҗж·ұеәҰжЁЎеһӢзҡ„еҶ…йғЁиЎЁеҫҒгҖӮиҝҷз§Қи·ЁеӯҰ科зҡ„иһҚеҗҲпјҢжңүжңӣдёәз ҙи§ЈзҘһз»ҸзҪ‘з»ңзҡ„вҖңй»‘зӣ’вҖқй—®йўҳжҸҗдҫӣжӣҙејәеӨ§гҖҒжӣҙйҖҡз”Ёзҡ„зҗҶи®әжӯҰеҷЁпјҢ并жҺЁеҠЁдәәе·ҘжҷәиғҪеҗ‘жӣҙеҸҜйқ гҖҒжӣҙеҸҜдҝЎиө–зҡ„ж–№еҗ‘еҸ‘еұ•гҖӮ