归纳偏置在Grokking现象中的作用与机制
从记忆到泛化的相变过程解析
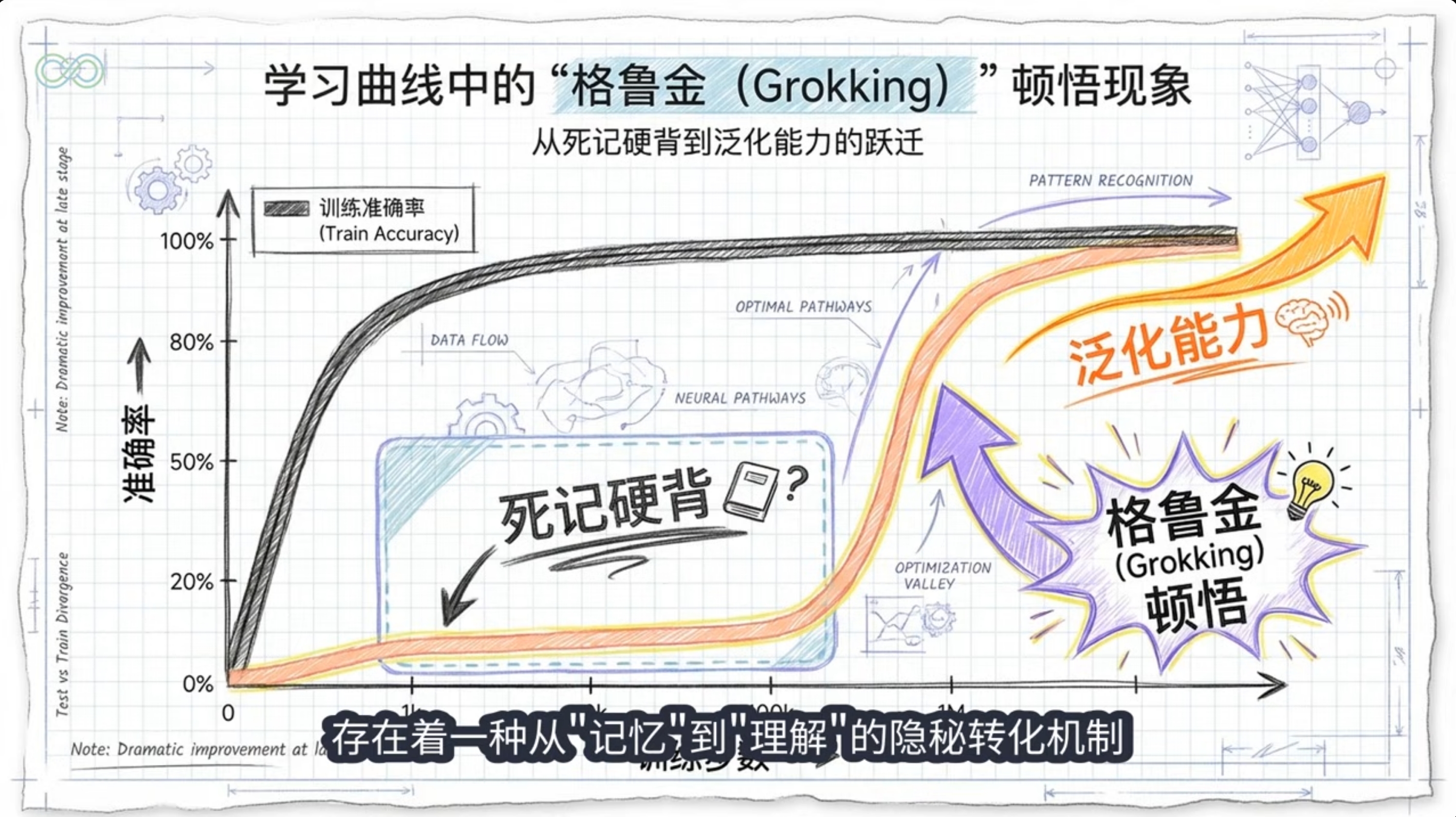
lightbulb 引言：Grokking现象简介
Grokking是指神经网络在训练集上完全过拟合后，经过长时间继续训练，突然在验证/测试集上实现快速泛化的现象。
- 典型特征：训练损失快速下降后停滞，测试准确率长时间随机水平后突跃
- 原始发现：2022年OpenAI论文《Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets》
- 关键条件：数据有限、强正则化、过参数化模型、超长训练
psychology 归纳偏置与Grokking
归纳偏置定义：学习算法对解空间的先验假设，使模型偏好某些函数而非其他
早期阶段
优化器隐式偏置或大初始化偏向"记忆解"(kernel regime)
arrow_forward
晚期阶段
权重衰减或优化器后期偏置转向"最小范数/最大边际解"(min-norm/max-margin)
arrow_forward
相变结果
早期偏置导致过拟合，晚期偏置导致泛化，形成尖锐相变
build 机制解释
electrical_services
电路竞争理论
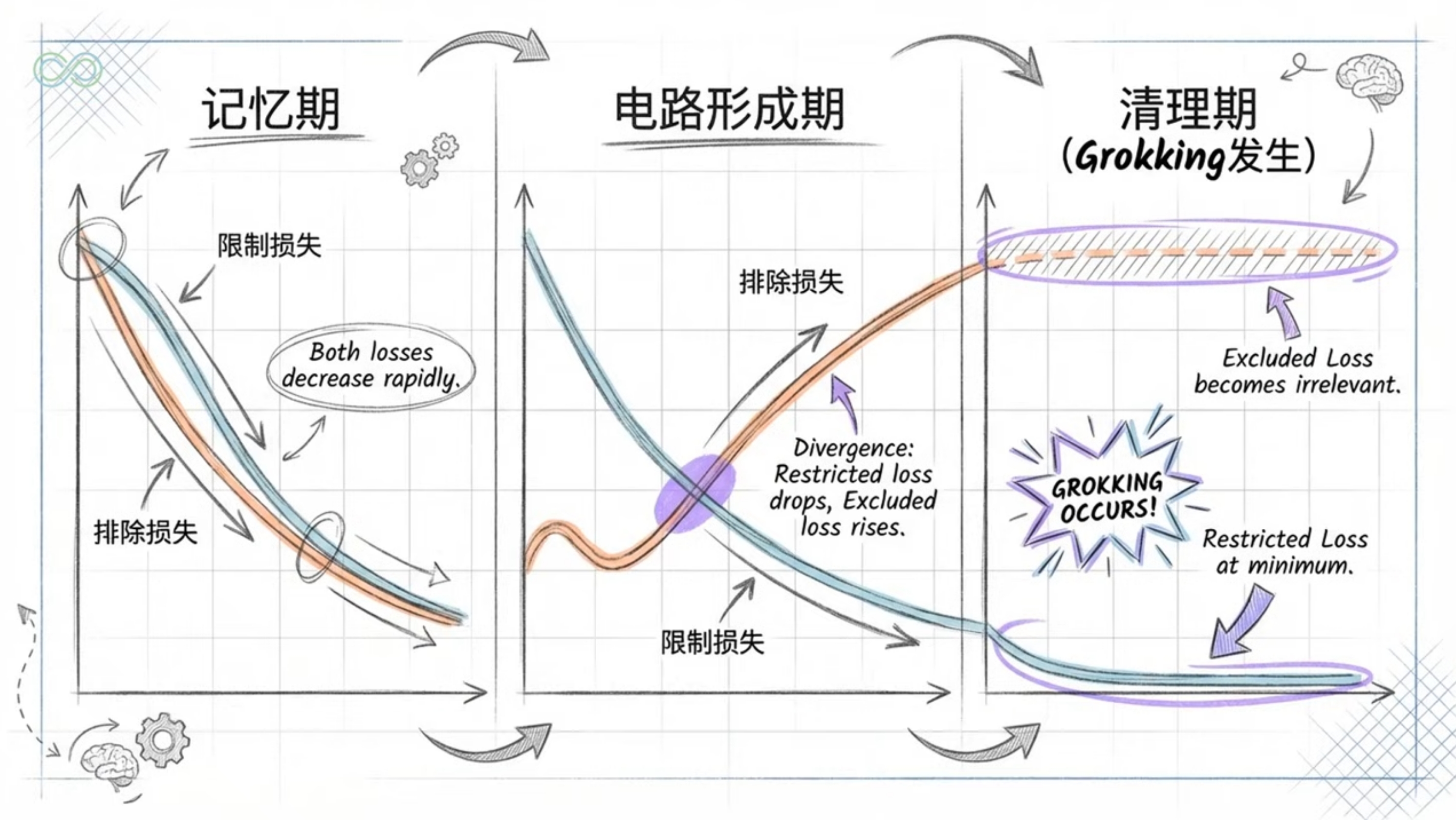
记忆电路vs泛化电路，权重衰减偏好更简洁的泛化电路。记忆电路在压缩大数据集方面效率低，而泛化电路有更大的固定成本但更好的每样本效率。
trending_down
复杂度动态
记忆阶段复杂度上升，泛化阶段复杂度下降。适当正则化的网络表现出尖锐的相变，而未正则化的网络则被困在高复杂度的记忆阶段。
speed
数值稳定性
Softmax Collapse导致梯度停滞，继续训练突破后突发更新。超过过拟合点后，梯度与"朴素损失最小化"(NLM)方向强烈对齐。
surfing
梯度冲浪
正则化使最小损失点集合更易于导航。在没有正则化的情况下，SGD不能轻易地在相同损失点之间移动，正则化释放了神经网络在损失盆地中"冲浪"的能力。
smart_toy 在LLM中的表现
- 异步局部Grokking：不同数据域异步进入grokking阶段，泛化在损失收敛后仍提升
- 隐式推理：transformer通过Grokking学习隐式推理能力，如组合和比较推理
- 系统性泛化：不同推理类型的泛化水平不同，组合推理的泛化能力低于比较推理
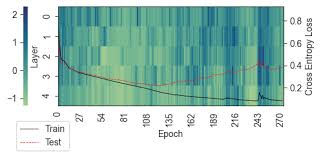
Grokking训练动态：训练损失与测试准确率随时间变化
new_releases 最新研究进展
- 电路效率理论：Varma et al. (2023)提出泛化电路逐渐胜过记忆电路是因为效率差异
- 复杂度相变：DeMoss et al. (2024)引入基于率失真理论的复杂度测量框架
- 数值稳定性视角：Prieto et al. (2025)发现Softmax Collapse阻止Grokking，并提出StableMax激活函数
- 隐式推理机制：Wang et al. (2024)揭示transformer通过Grokking形成"泛化电路"实现隐式推理
tips_and_updates 应用与启示
tune
训练优化
调整初始化规模、权重衰减与优化器，监控电路/秩演化作为Grokking指标。适度延长训练并加强正则化，可能诱导更好泛化。
precision_manufacturing
效率提升
利用归纳偏置提取与匹配策略优化提示工程。使用Adam等自适应优化器并延长训练，结合合适正则化诱导更好泛化。
summarize 结论
归纳偏置是Grokking机制的核心驱动力：训练早期隐式/显式偏置倾向记忆化解（快速拟合），晚期偏置（如权重衰减驱动的最小范数、电路效率，或优化器Slingshot）转向简洁泛化解，导致从过拟合到延迟泛化的尖锐相变。2023-2025研究证实阶段二分偏置可严谨证明Grokking，并在LLM中表现为局部异步现象，为理解涌现能力提供新视角。